Topics

• Sampling distributions and the Central Limit Theorem

• Hypothesis test to test a claim about a population parameter

• Confidence interval to estimate a population parameter

Terminology

Population: a group of individuals or objects we are interested in studying

Parameter: a numerical quantity derived from the population (almost always unknown)

If we had data from every unit in the population, we could just calculate population parameters and be done!

Unfortunately, we usually cannot do this.

Sample: a subset of our population of interest

Statistic: a numerical quantity derived from a sample

Inference

If the sample is representative, then we can use the tools of probability and statistical inference to make generalizable conclusions to the broader population of interest.

Similar to tasting a spoonful of soup while cooking to make an inference about the entire pot.

Statistical inference

Statistical inference is the process of using sample data to make conclusions about the underlying population the sample came from.

• Estimation: using the sample to estimate a plausible range of values for the unknown parameter

• Testing: evaluating whether our observed sample provides evidence for or against some claim about the population

Let's *virtually* go to Asheville!

Asheville data

Inside Airbnb scraped all Airbnb listings in Asheville, NC, that were active on June 25, 2020.

Population of interest: listings in the Asheville with at least ten reviews.

Parameter of interest: Mean price per guest per night among these listings.

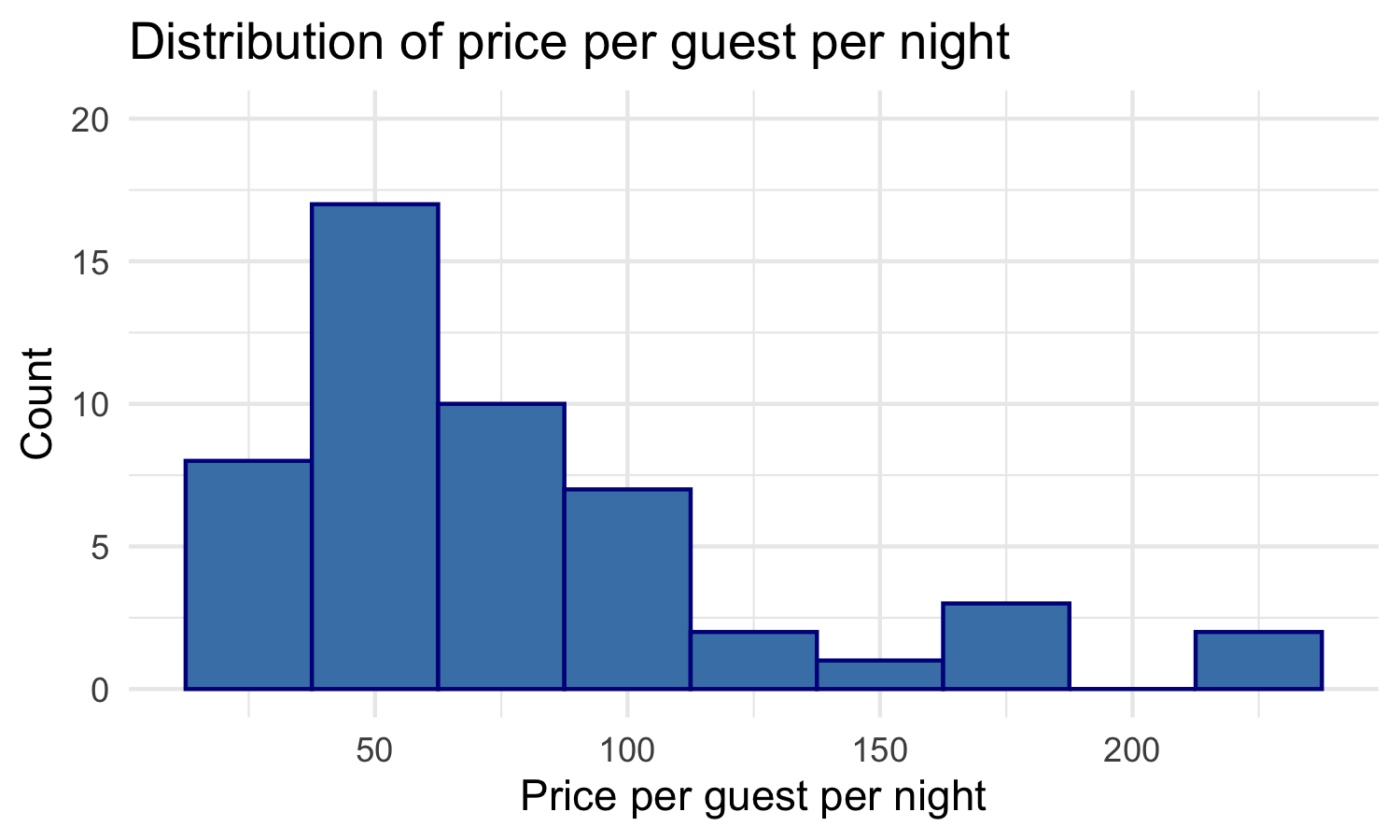
Visualizing our sample

We have data on the price per guest (ppg) for a random sample of 50 Airbnb listings.

Sample statistic

A sample statistic (point estimate) is a single value of a statistic computed from the sample data to serve as the "best guess", or estimate, for the population parameter.

abb %>% 
  summarize(mean_price = mean(ppg))

## # A tibble: 1 x 1
##   mean_price
##        <dbl>
## 1       76.6

If we took another random sample of 50 Airbnbs in Asheville, we'd likely have a different sample statistic.

Variability of sample statistics

• Each sample from the population yields a slightly different sample statistic.

• The sample-to-sample difference is called sampling variability.

• We can use theory to help us understand the underlying sampling distribution and quantify this sample-to-sample variability.

The goal of statistical inference

• Statistical inference is the act of generalizing from a sample in order to make conclusions regarding a population.

• We are interested in population parameters, which we do not observe. Instead, we must calculate statistics from our sample in order to learn about them.

• As part of this process, we must quantify the degree of uncertainty in our sample statistic.

Sampling distribution of the mean

We're interested in the mean price per guest per night at Aribnbs in Asheville, so suppose we were able to do the following:

1. Take a random sample of size n from this population, and calculate the mean price per guest per night in this sample, ˉX1

2. Put the sample back, take a second random sample of size n, and calculate the mean price per guest per night from this new sample, ˉX2

3. Put the sample back, take a third random sample of size n, and calculate the mean price per guest per night from this sample, too...

...and so on.

Sampling distribution of the mean

After repeating this many times, we have a dataset that has the K sample averages from the population: ˉX1, ˉX2, ⋯, ˉXK

The Central Limit Theorem

For a population with a well-defined mean μ and standard deviation σ, these three properties hold for the distribution of sample average ˉX, assuming certain conditions hold:

1. The mean of the sampling distribution of the mean is identical to the population mean μ.

2. The standard deviation of the distribution of the sample averages is σ/√n.

   • This is called the standard error (SE) of the mean.

3. For n large enough, the shape of the sampling distribution of means is approximately normally distributed.

The normal (Gaussian) distribution

The normal distribution is unimodal and symmetric and is described by its density function:

If a random variable X follows the normal distribution, then f(x)=1√2πσ2exp{−12(x−μ)2σ2}

The normal distribution (graphically)

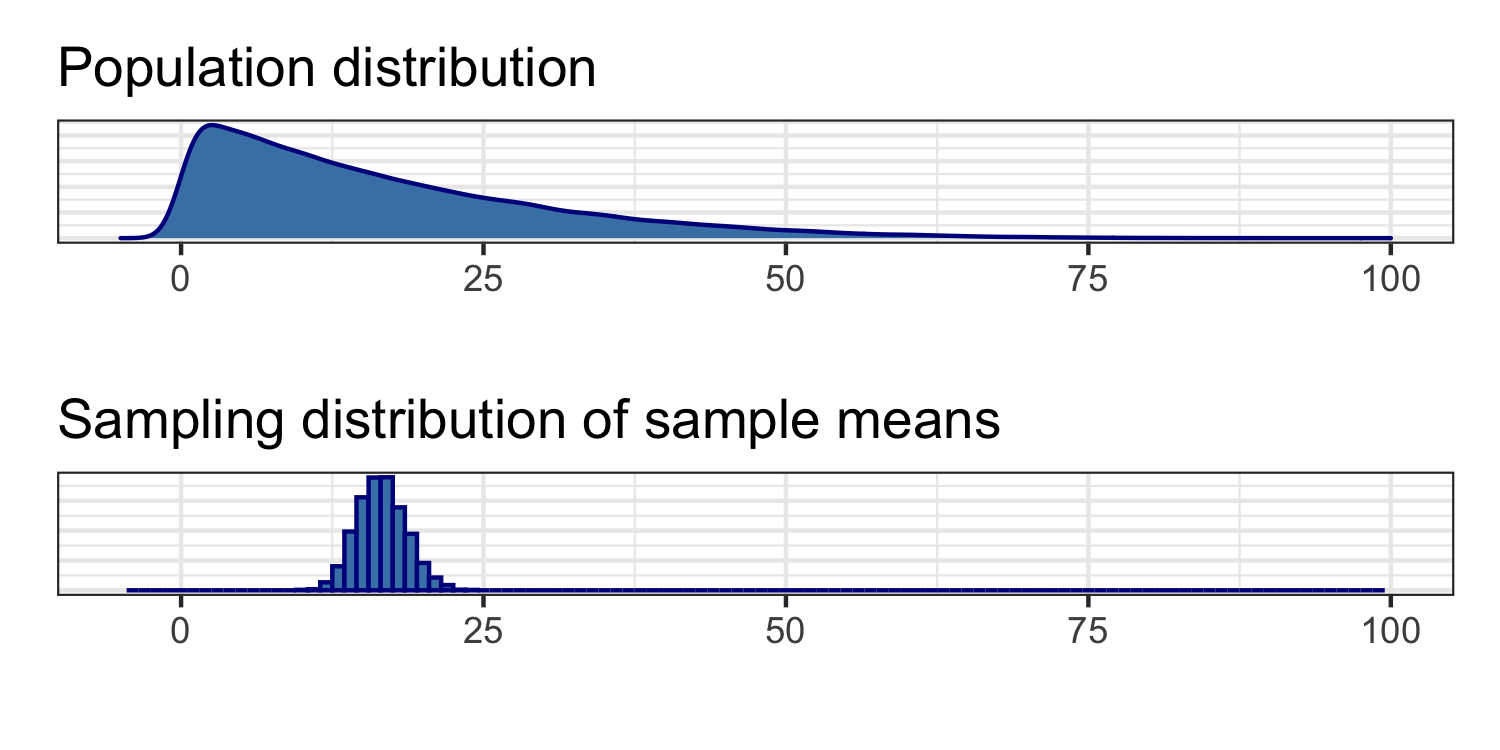
Wait, any population distribution?

The Central Limit Theorem tells us that sample means are normally distributed, if we have enough data and certain conditions hold.

This is true even if the population distribution is not normally distributed.

Click here to see an interactive demonstration of this idea.

Conditions for CLT

We need to check two conditions for CLT to hold: independence, sample size/distribution.

✅ Independence: The sampled observations must be independent. This is difficult to check, but the following are useful guidelines:

• the sample must be randomly taken
• if sampling without replacement, sample size must be less than 10% of the population size

If samples are independent, then by definition one sample's value does not "influence" another sample's value.

Conditions for CLT

✅ Sample size / distribution:

• if data are numerical, usually n > 30 is considered a large enough sample for the CLT to kick in
• if we know for sure that the underlying data are normally distributed, then the distribution of sample averages will also be exactly normal, regardless of the sample size
• if data are categorical, at least 10 successes and 10 failures.

Underlying population (not observed in real life!)

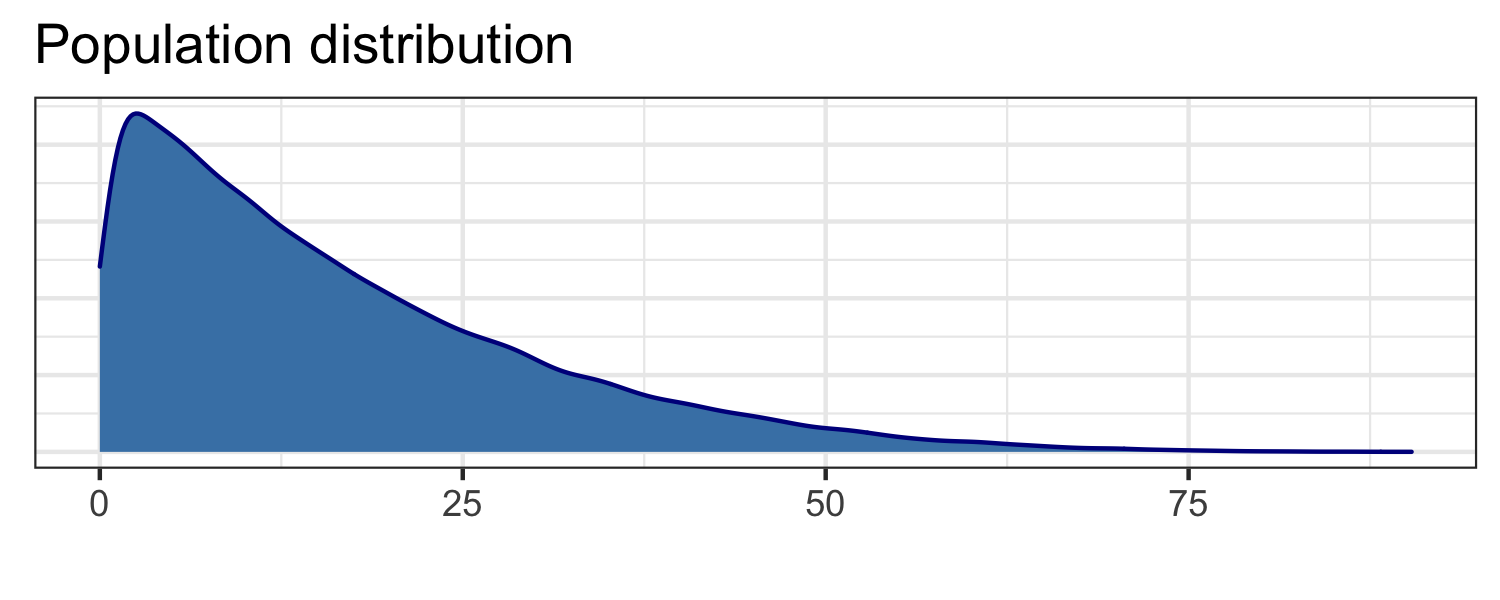
## # A tibble: 1 x 2
##      mu sigma
##   <dbl> <dbl>
## 1  16.6  14.0

Sampling from the population - 1

set.seed(1)
samp_1 <- rs_pop %>%
  sample_n(size = 50) %>%
  summarise(x_bar = mean(x))

samp_1

## # A tibble: 1 x 1
##   x_bar
##   <dbl>
## 1  16.4

Sampling from the population - 2

set.seed(2)
samp_2 <- rs_pop %>%
  sample_n(size = 50) %>% 
  summarise(x_bar = mean(x))

samp_2

## # A tibble: 1 x 1
##   x_bar
##   <dbl>
## 1  13.3

Sampling from the population - 3

set.seed(3)
samp_3 <- rs_pop %>%
  sample_n(size = 50) %>% 
  summarise(x_bar = mean(x))

samp_3

## # A tibble: 1 x 1
##   x_bar
##   <dbl>
## 1  17.8

keep repeating...

Sampling distribution

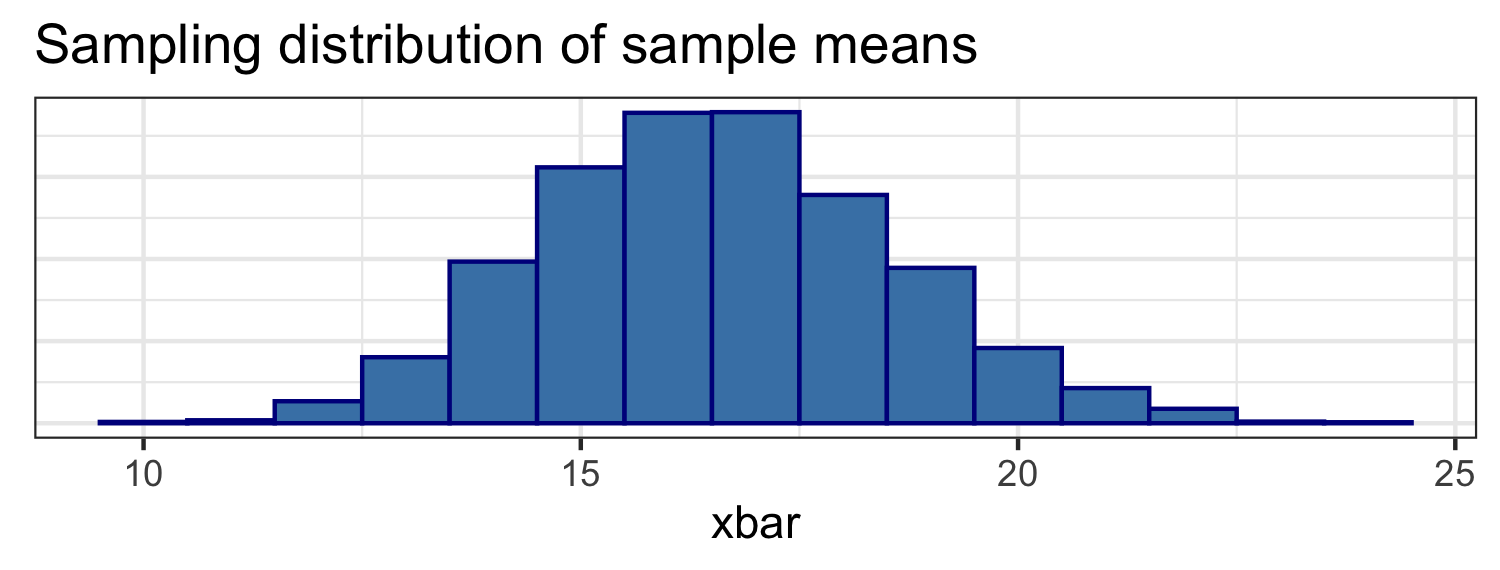
## # A tibble: 1 x 2
##    mean    se
##   <dbl> <dbl>
## 1  16.6  2.02

CLT Recap

• If certain conditions are satisfied, regardless of the shape of the population distribution, the sampling distribution of the mean follows an approximately normal distribution.

• The center of the sampling distribution is at the center of the population distribution.

• The sampling distribution is less variable than the population distribution (and we can quantify by how much).

Back to Asheville

✅ Independence

• The Airbnbs in this data set were randomly selected
• 50 is less than 10% of all Airbnbs in Asheville

✅ Sample size / distribution

• The sample size 50 is sufficiently large, (n>30)

Back to Asheville

• We will use the CLT to draw conclusions about μ, and we'll deal with the unknown σ.

Why do we care?

Knowing the distribution of the sample statistic ˉX can help us

• estimate a population parameter as sample statistic ± margin of error

  • the margin of error is comprised of a measure of how confident we want to be and how variable the sample statistic is
    

• test for a population parameter by evaluating how likely it is to obtain to observed sample statistic when assuming that the null hypothesis is true

  • this probability will depend on how variable the sampling distribution is

Inference based on the CLT

If necessary conditions are met, we can also use inference methods based on the CLT. Suppose we know the true population standard deviation.

Then the CLT tells us that ˉX approximately has the distribution N(μ,σ/√n).

That is,

Z=ˉX−μσ/√n∼N(0,1)

What if σ isn't known?

T distribution

• In practice, we never know the true value of σ, and so we estimate it from our data with s.

• In practice We will use the t distribution instead of the standard normal distribution when we conduct statistical inference for the mean (and eventually linear regression coefficients)

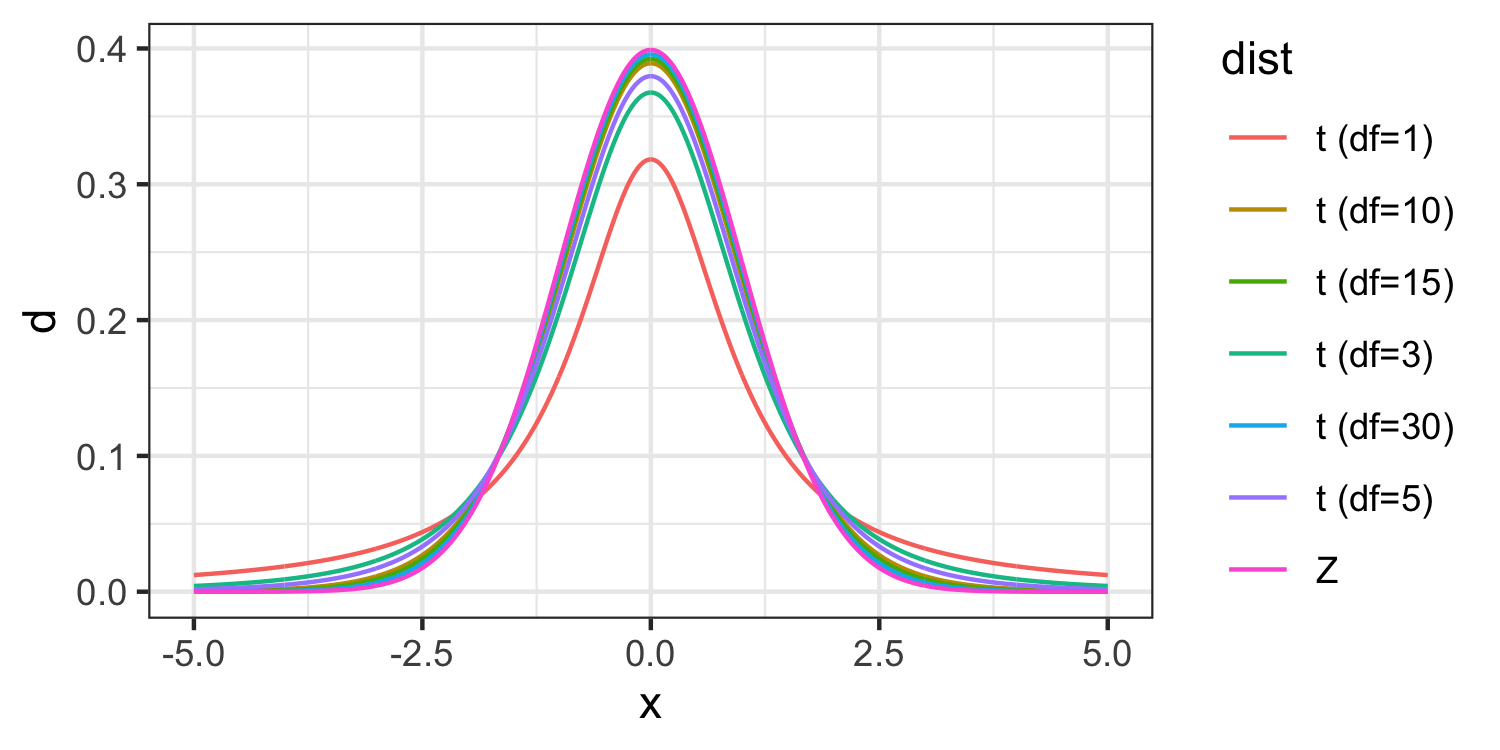
T distribution

The t-distribution is also unimodal and symmetric, and is centered at 0

Thicker tails than the normal distribution

• This is to make up for additional variability introduced by using s instead of σ in calculation of the standard error (SE), s/√n.

T vs Z distributions

Mean price per guest per night

Outline of a hypothesis test

1️⃣ State the hypotheses.

2️⃣ Calculate the test statistic.

3️⃣ Calculate the p-value.

4️⃣ State the conclusion.

1️⃣ State the hypotheses

• We define the hypotheses before analyzing the data.

• We will assume the null hypothesis is true and assess the strength of evidence against the null hypohtesis.

2️⃣ Calculate the test statistic.

From our data

2️⃣ Calculate the test statistic.

From our data

3️⃣ Calculate the p-value.

The p-value is the probability of observing a test statistic at least as extreme as the one we've observed, given the null hypothesis is true.

3️⃣ Calculate the p-value

The test statistic follows a t distribution with 49 degrees of freedom.

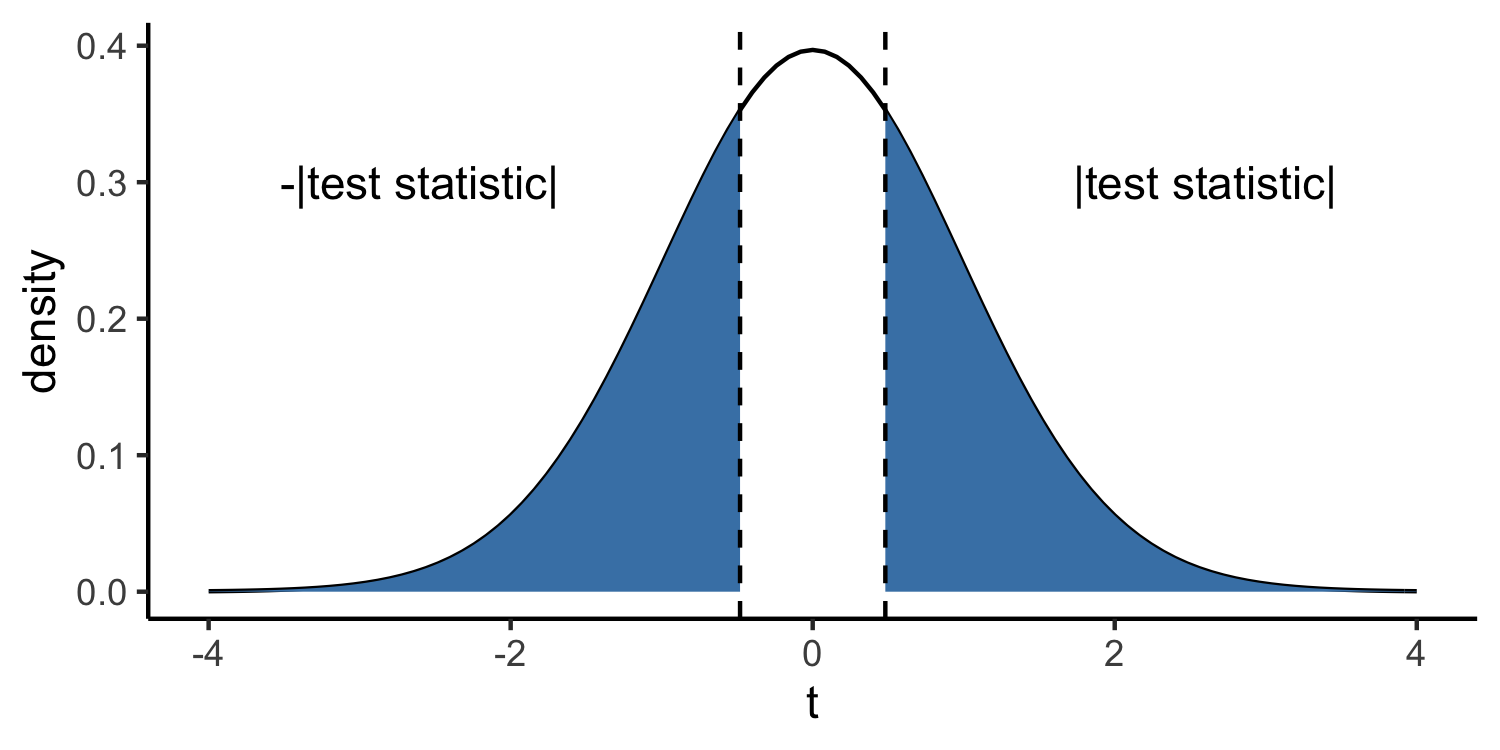
pval <- 2 * pt(abs(-0.481), 49, 
               lower.tail = FALSE)
pval

## [1] 0.6326574

Understanding the p-value

These are general guidelines. The strength of evidence depends on the context of the problem.

4️⃣ State the conclusion

The p-value of 0.633 is large, so we fail to reject the null hypothesis.

The data do not provide sufficient evidence that the mean price per guest per night for Airbnbs in Asheville is not equal to $80.

Confidence interval

t∗ is calculated from a t distribution with n−1 degrees of freedom

Calculating the 95% CI for μ

t_star <- qt(0.975, 49)
t_star

## [1] 2.009575

Interpretation

We are 95% confident the true mean price per guest per night for Airbnbs in Asheville is between $62.33 and $90.84.

Note that this is consistent with the conclusion from our hypothesis test.

One-sample t-test functions in R (both work!)

library(infer)
t_test(abb, response = ppg, mu = 80)

## # A tibble: 1 x 6
##   statistic  t_df p_value alternative lower_ci upper_ci
##       <dbl> <dbl>   <dbl> <chr>          <dbl>    <dbl>
## 1    -0.481    49   0.632 two.sided       62.3     90.8

t.test(abb$ppg, mu = 80) %>%
  tidy()

## # A tibble: 1 x 8
##   estimate statistic p.value parameter conf.low conf.high method     alternative
##      <dbl>     <dbl>   <dbl>     <dbl>    <dbl>     <dbl> <chr>      <chr>      
## 1     76.6    -0.481   0.632        49     62.3      90.8 One Sampl… two.sided

Recap

• Sampling distributions and the Central Limit Theorem

• Hypothesis test to test a claim about a population parameter

• Confidence interval to estimate a population parameter

Acknowledgements

Some slides were adapted from Data Science in a Box.