Comparing means with ANOVA
Prof. Maria Tackett
Topics
Topics
- Compare groups using analysis of variance
Topics
- Compare groups using analysis of variance
Aldrin in the Wolf River
The Wolf River in Tennessee flows past an abandoned site once used by the pesticide industry for dumping wastes, including chlordane (pesticide), aldrin, and dieldrin (both insecticides).
These highly toxic organic compounds can cause various cancers and birth defects.
Aldrin in the Wolf River
## # A tibble: 30 x 2## aldrin depth ## <dbl> <chr> ## 1 3.8 bottom## 2 4.8 bottom## 3 4.9 bottom## 4 5.3 bottom## 5 5.4 bottom## 6 5.7 bottom## 7 6.3 bottom## 8 7.3 bottom## 9 8.1 bottom## 10 8.8 bottom## # … with 20 more rows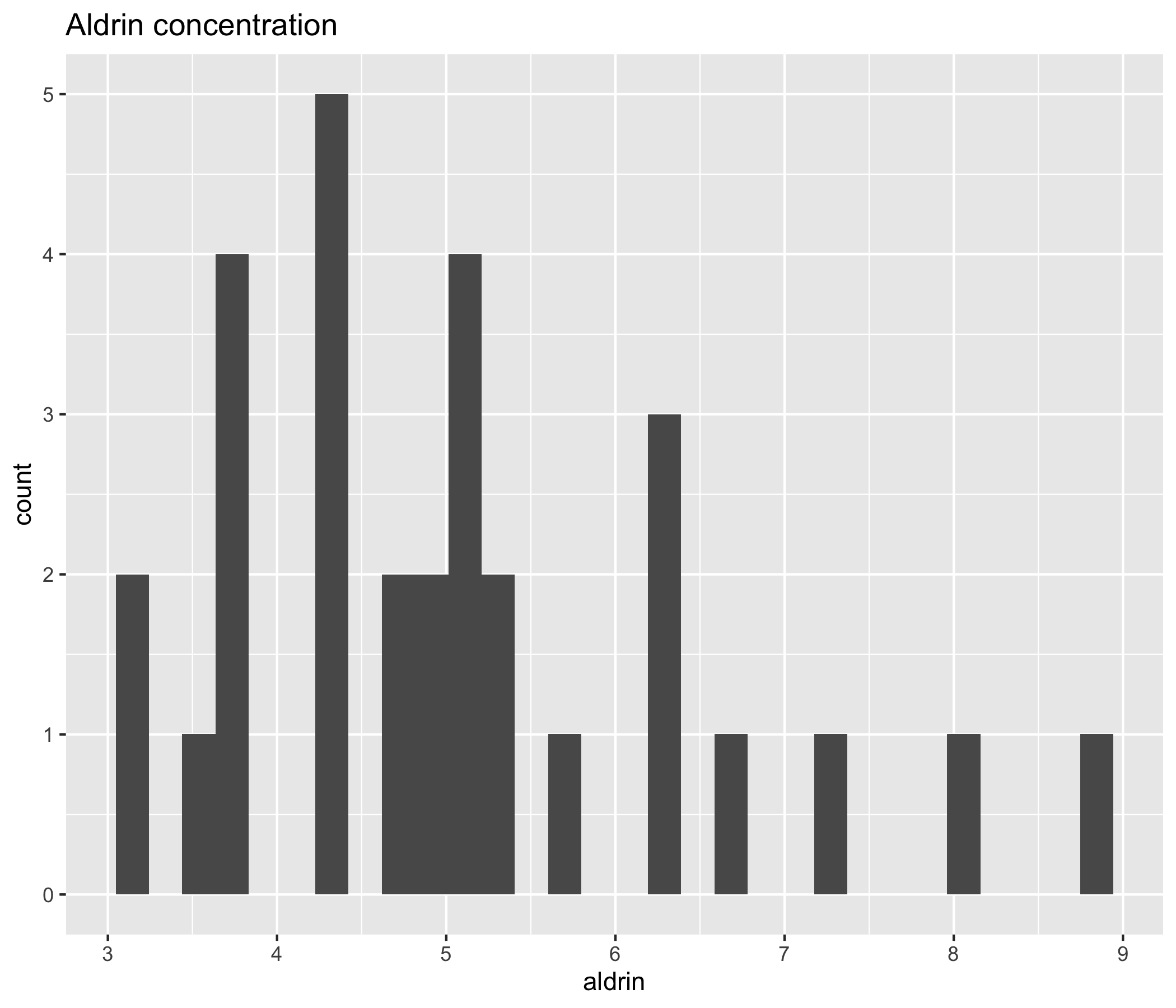
Aldrin in the Wolf River
- The standard methods to test whether these substances are present in a river is to take samples at six-tenths depth.
- These compounds are denser than water and their molecules tend to stick to particles of sediment, they are more likely to be found in higher concentrations near the bottom than near mid-depth.
Is there a difference between the mean aldrin concentrations among the three depth levels?
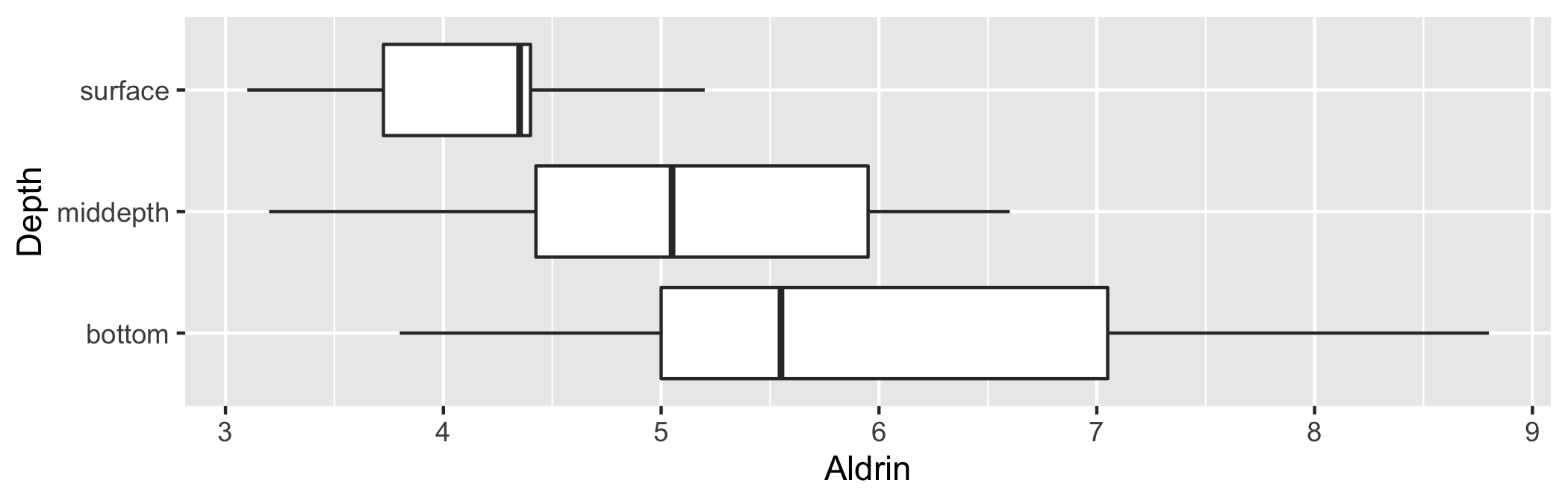
Aldrin by depth
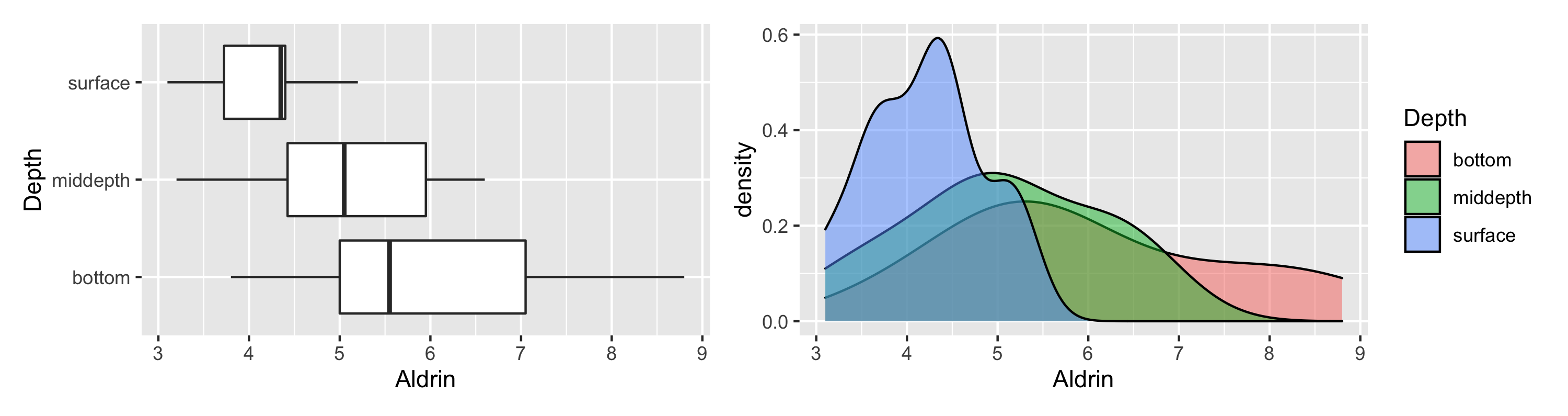
| depth | n | mean | sd |
|---|---|---|---|
| bottom | 10 | 6.04 | 1.579 |
| middepth | 10 | 5.05 | 1.104 |
| surface | 10 | 4.20 | 0.660 |
So far, we have used a quantitative predictor variable to understand the variation in a quantitative response variable.
Now, we will use a categorical (qualitative) predictor variable to understand the variation in a quantitative response variable.
Notation
- K is number of mutually exclusive groups. We index the groups as i=1,…,K.
Notation
K is number of mutually exclusive groups. We index the groups as i=1,…,K.
ni is number of observations in group i
Notation
K is number of mutually exclusive groups. We index the groups as i=1,…,K.
ni is number of observations in group i
n=n1+n2+⋯+nK is the total number of observations in the data
Notation
K is number of mutually exclusive groups. We index the groups as i=1,…,K.
ni is number of observations in group i
n=n1+n2+⋯+nK is the total number of observations in the data
yij is the jth observation in group i, for all i,j
Notation
K is number of mutually exclusive groups. We index the groups as i=1,…,K.
ni is number of observations in group i
n=n1+n2+⋯+nK is the total number of observations in the data
yij is the jth observation in group i, for all i,j
μi is the population mean for group i, for i=1,…,K
Using ANOVA to compare means
Question of interest Is the mean value of the response y the same for all groups, or is there at least one group with a significantly different mean value?
To answer this question, we will test the following hypotheses:
H0:μ1=μ2=⋯=μKHa:At least one μi is not equal to the others
What's happening...
H0:μ1=μ2=⋯=μKHa:At least one μi is not equal to the others
- If the sample means are "far apart", " there is evidence against H0
- We will calculate a test statistic to quantify "far apart" in the context of the data
Analysis of Variance (ANOVA)
Main Idea: Decompose the total variation in the data into the variation between groups (model) and the variation within each group (residuals)
K∑i=1ni∑j=1(yij−ˉy)2=K∑i=1ni(ˉyi−ˉy)2+K∑i=1ni∑j=1(yij−ˉyi)2
Analysis of Variance (ANOVA)
Main Idea: Decompose the total variation in the data into the variation between groups (model) and the variation within each group (residuals)
K∑i=1ni∑j=1(yij−ˉy)2=K∑i=1ni(ˉyi−ˉy)2+K∑i=1ni∑j=1(yij−ˉyi)2
- If the variation between groups is significantly greater than the variation within each group, then there is evidence against the null hypothesis.
ANOVA table
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| depth | 2 | 16.961 | 8.480 | 6.134 | 0.006 |
| Residuals | 27 | 37.329 | 1.383 |
Total variation
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| depth | 2 | 16.961 | 8.480 | 6.134 | 0.006 |
| Residuals | 27 | 37.329 | 1.383 |
Total variation
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| depth | 2 | 16.961 | 8.480 | 6.134 | 0.006 |
| Residuals | 27 | 37.329 | 1.383 |
Total variation: variation between and within groups
SSTotal=16.961+37.329=54.290
DFTotal=2+37=29
s2y=SSTotalDFTotal=54.29029=1.872
Between variation
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| depth | 2 | 16.961 | 8.480 | 6.134 | 0.006 |
| Residuals | 27 | 37.329 | 1.383 |
Between variation
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| depth | 2 | 16.961 | 8.480 | 6.134 | 0.006 |
| Residuals | 27 | 37.329 | 1.383 |
Between variation: variation in the group means
SSBetween=16.961
DFBetween=2
MSBetween=SSBetweenDFBetween=15.9612=8.480
Within variation
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| depth | 2 | 16.961 | 8.480 | 6.134 | 0.006 |
| Residuals | 27 | 37.329 | 1.383 |
Within variation
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| depth | 2 | 16.961 | 8.480 | 6.134 | 0.006 |
| Residuals | 27 | 37.329 | 1.383 |
Within variation: variation within each group
SSWithin=37.329
DFWithin=27
MSWithin=SSWithinDFWithin=37.32927=1.383
Using ANOVA table to test difference in means
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| depth | 2 | 16.961 | 8.480 | 6.134 | 0.006 |
| Residuals | 27 | 37.329 | 1.383 |
H0:μ1=μ2=μ3Ha:At least one depth level has μi that is not equal to the others
Using ANOVA table to test difference in means
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| depth | 2 | 16.961 | 8.480 | 6.134 | 0.006 |
| Residuals | 27 | 37.329 | 1.383 |
Test statistic: Ratio of between group and within group variation
F=MSBetweenMSWithin=8.4801.383=6.134
Calculate p-value
Calculate the p-value using an F distribution with K−1 and n−K degrees of freedom
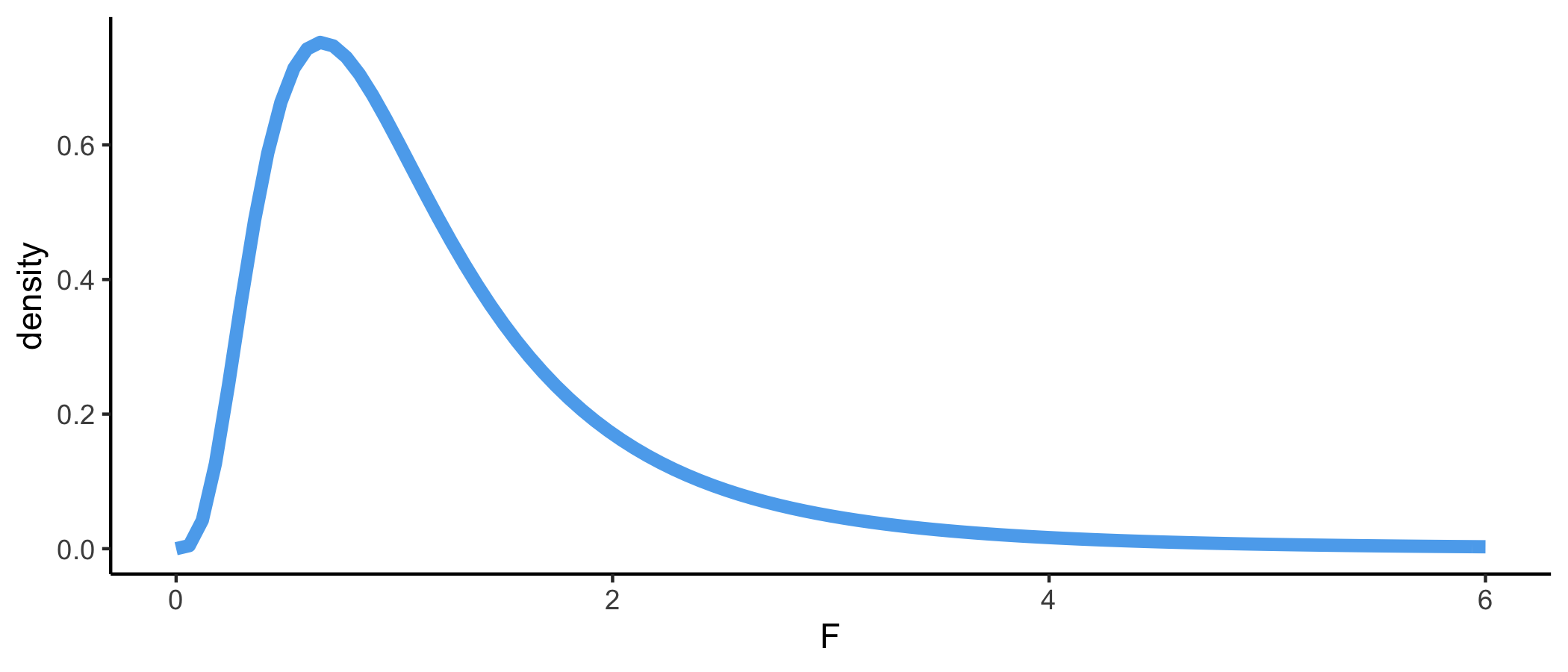
Using ANOVA table to test difference in means
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| depth | 2 | 16.961 | 8.480 | 6.134 | 0.006 |
| Residuals | 27 | 37.329 | 1.383 |
P-value: Probability of observing a test statistic at least as extreme as F Stat given the group means are equal
Using ANOVA table to test difference in means
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| depth | 2 | 16.961 | 8.480 | 6.134 | 0.006 |
| Residuals | 27 | 37.329 | 1.383 |
P-value: Probability of observing a test statistic at least as extreme as F Stat given the group means are equal
The p-value is very small (≈0), so we reject H0. The data provide sufficient evidence that at least one depth level has a mean aldrin concentration that differs from the others.
Assumptions for ANOVA
Assumptions for ANOVA
Assumptions for ANOVA
1️⃣ Normality: yij∼N(μi,σ2)
Assumptions for ANOVA
1️⃣ Normality: yij∼N(μi,σ2)
2️⃣ Constant variance: The population distribution for each group has a common variance, σ2
Assumptions for ANOVA
1️⃣ Normality: yij∼N(μi,σ2)
2️⃣ Constant variance: The population distribution for each group has a common variance, σ2
3️⃣ Independence: The observations are independent from each other
- This applies to observations within and between groups
Assumptions for ANOVA
1️⃣ Normality: yij∼N(μi,σ2)
2️⃣ Constant variance: The population distribution for each group has a common variance, σ2
3️⃣ Independence: The observations are independent from each other
- This applies to observations within and between groups
For ANOVA, we can typically check these assumptions in the exploratory data analysis
Checking Normality
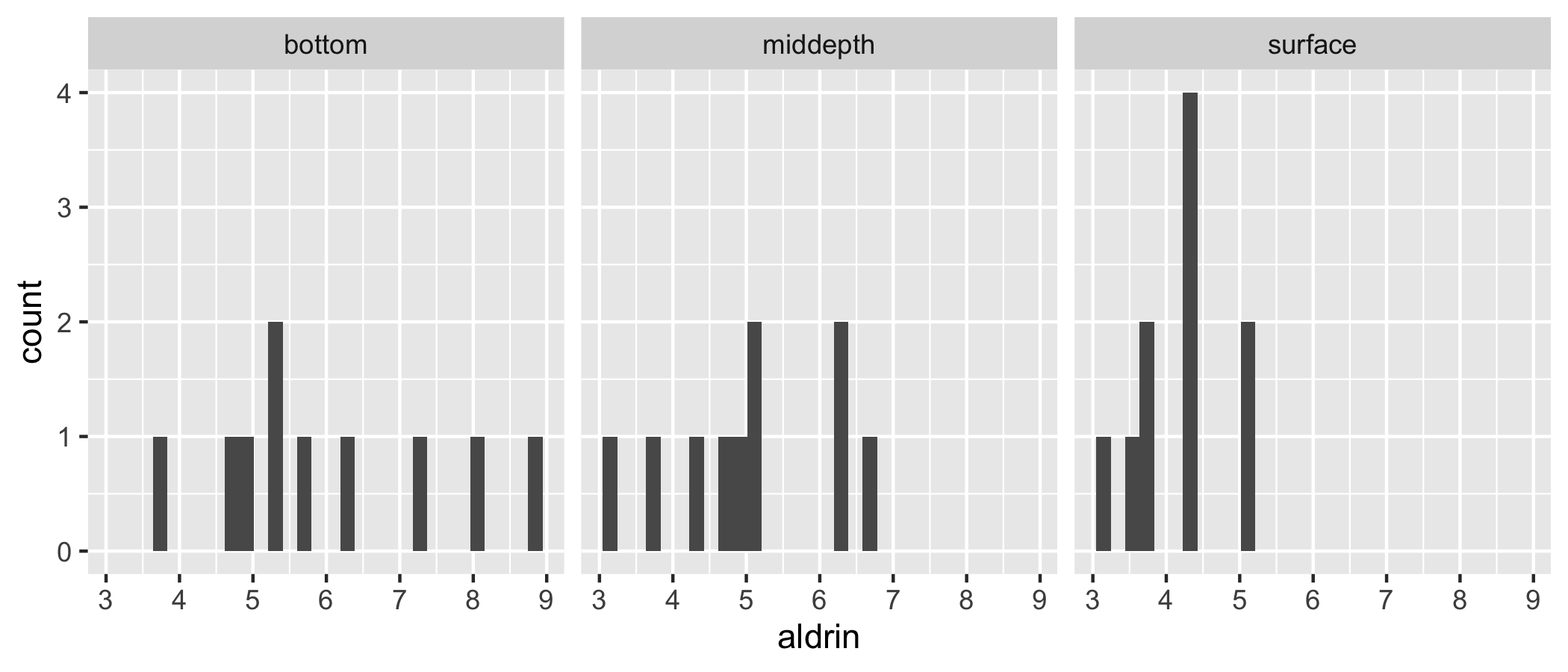
✅ No major skewness or outliers.
Checking Normality
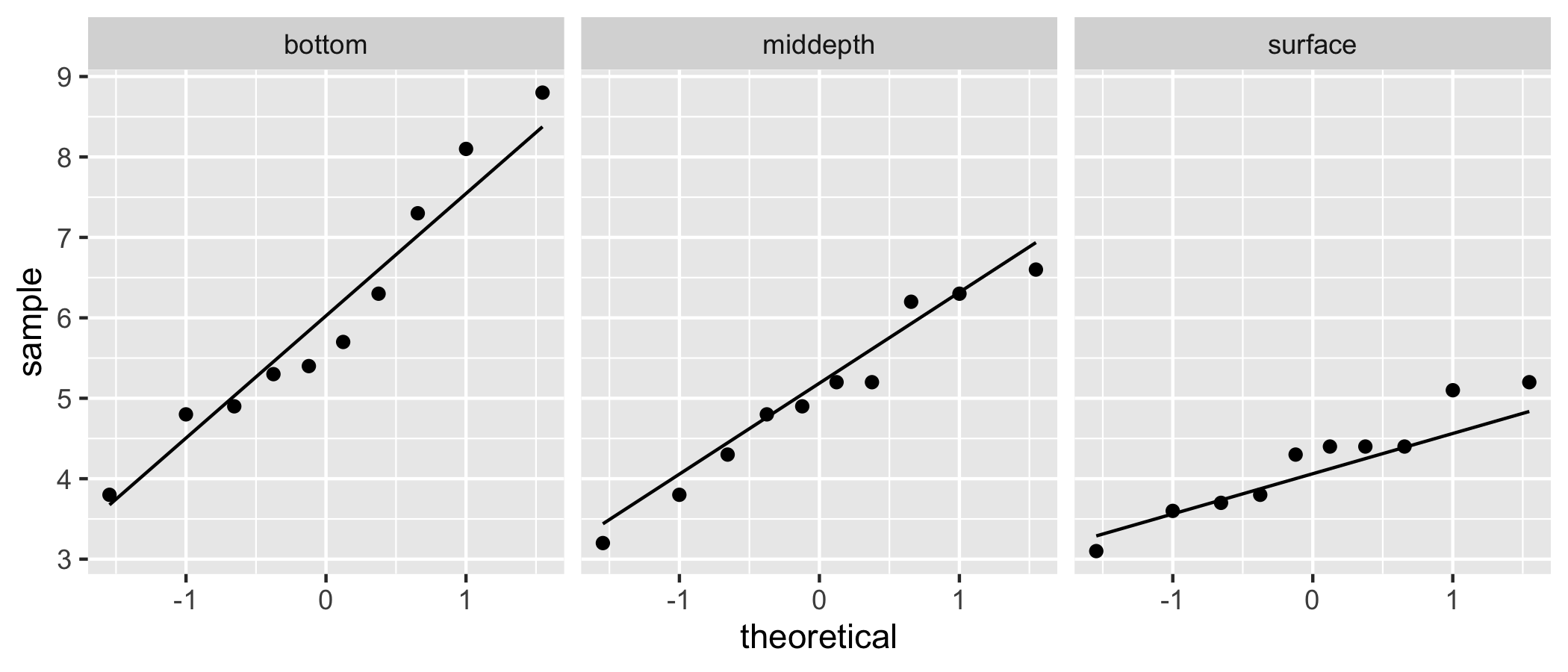
✅ Points fall relatively along the diagonal line.
Checking constant variance
## # A tibble: 3 x 4## depth n mean sd## * <chr> <int> <dbl> <dbl>## 1 bottom 10 6.04 1.58 ## 2 middepth 10 5.05 1.10 ## 3 surface 10 4.2 0.660✅ The maximum standard deviation is about 2.4 times the smallest one. This is OK given the small sample size.
Checking independence
✅ Based on what we know about the study, we have no reason to believe that the aldrin concentrations are not independent of each other.
Robustness to Assumptions
Robustness to Assumptions
- Normality: yij∼N(μi,σ2)
- ANOVA relatively robust to departures from Normality.
- Concern when there are strongly skewed distributions with different sample sizes (especially if sample sizes are small, < 10 in each group)
Robustness to Assumptions
Normality: yij∼N(μi,σ2)
- ANOVA relatively robust to departures from Normality.
- Concern when there are strongly skewed distributions with different sample sizes (especially if sample sizes are small, < 10 in each group)
Independence: There is independence within and across groups
- If this doesn't hold, should use methods that account for correlated errors
Robustness to Assumptions
- Constant variance: The population distribution for each group has a common variance, σ2
- Critical assumption, since the pooled (combined) variance is important for ANOVA
- General rule: Satisfied if SDmax/SDmin≤2. OK if this is somewhat >2 when sample sizes are small.
Recap
Recap
- Used ANOVA to compare means across groups