Checking conditions for MLR
Prof. Maria Tackett
Example: SAT Averages by State
This data set contains the average SAT score (out of 1600) and other variables that may be associated with SAT performance for each of the 50 U.S. states. The data is based on test takers for the 1982 exam.
Response variable:
SAT: average total SAT score
Data comes from case1201 data set in the Sleuth3 package
SAT Averages: Predictors
Takers: percentage of high school seniors who took examIncome: median income of families of test-takers ($ hundreds)Years: average number of years test-takers had formal education in social sciences, natural sciences, and humanitiesPublic: percentage of test-takers who attended public high schoolsExpend: total state expenditure on high schools ($ hundreds per student)Rank: median percentile rank of test-takers within their high school classes
Model
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -94.659 | 211.510 | -0.448 | 0.657 |
| Takers | -0.480 | 0.694 | -0.692 | 0.493 |
| Income | -0.008 | 0.152 | -0.054 | 0.957 |
| Years | 22.610 | 6.315 | 3.581 | 0.001 |
| Public | -0.464 | 0.579 | -0.802 | 0.427 |
| Expend | 2.212 | 0.846 | 2.615 | 0.012 |
| Rank | 8.476 | 2.108 | 4.021 | 0.000 |
Model conditions
Linearity: There is a linear relationship between the response and predictor variables.
Constant Variance: The variability about the least squares line is generally constant.
Normality: The distribution of the residuals is approximately normal.
Independence: The residuals are independent from each other.
Residuals vs. predicted values
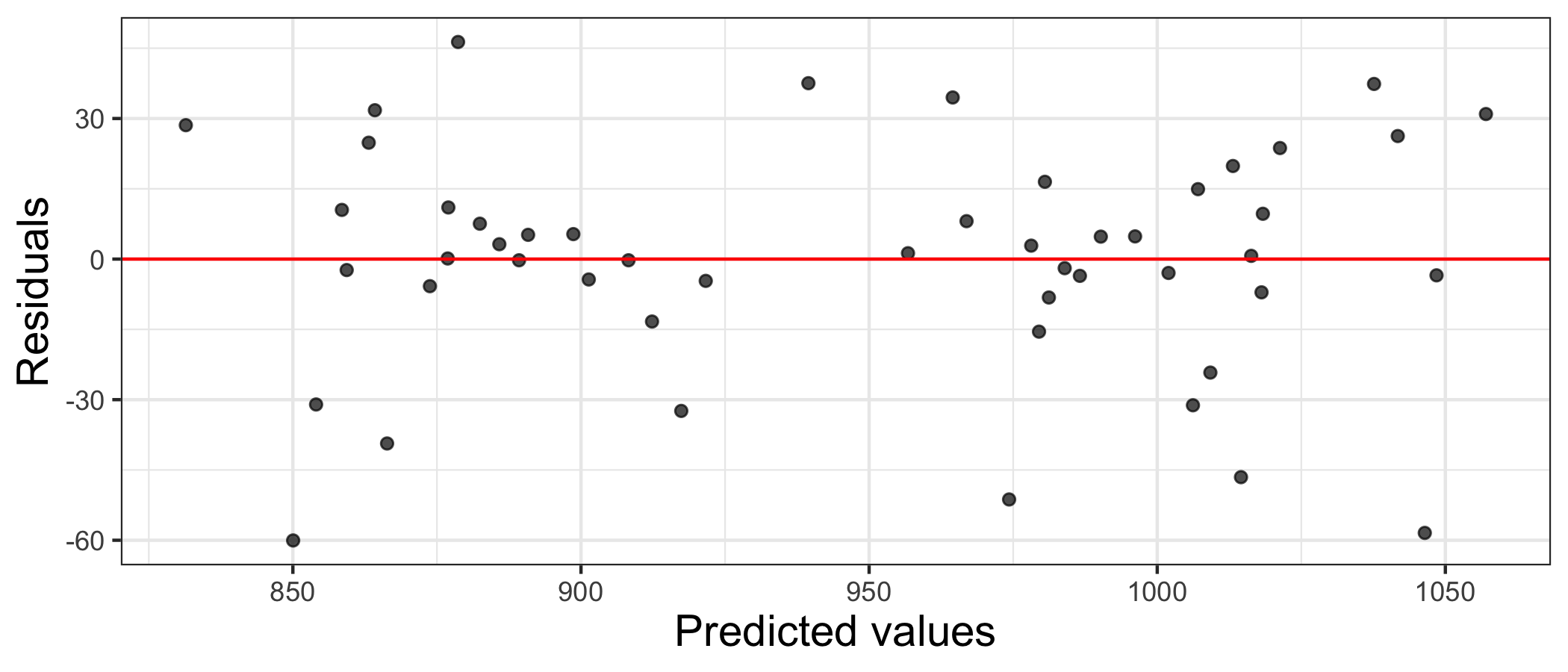
Linearity: Residuals vs. predicted
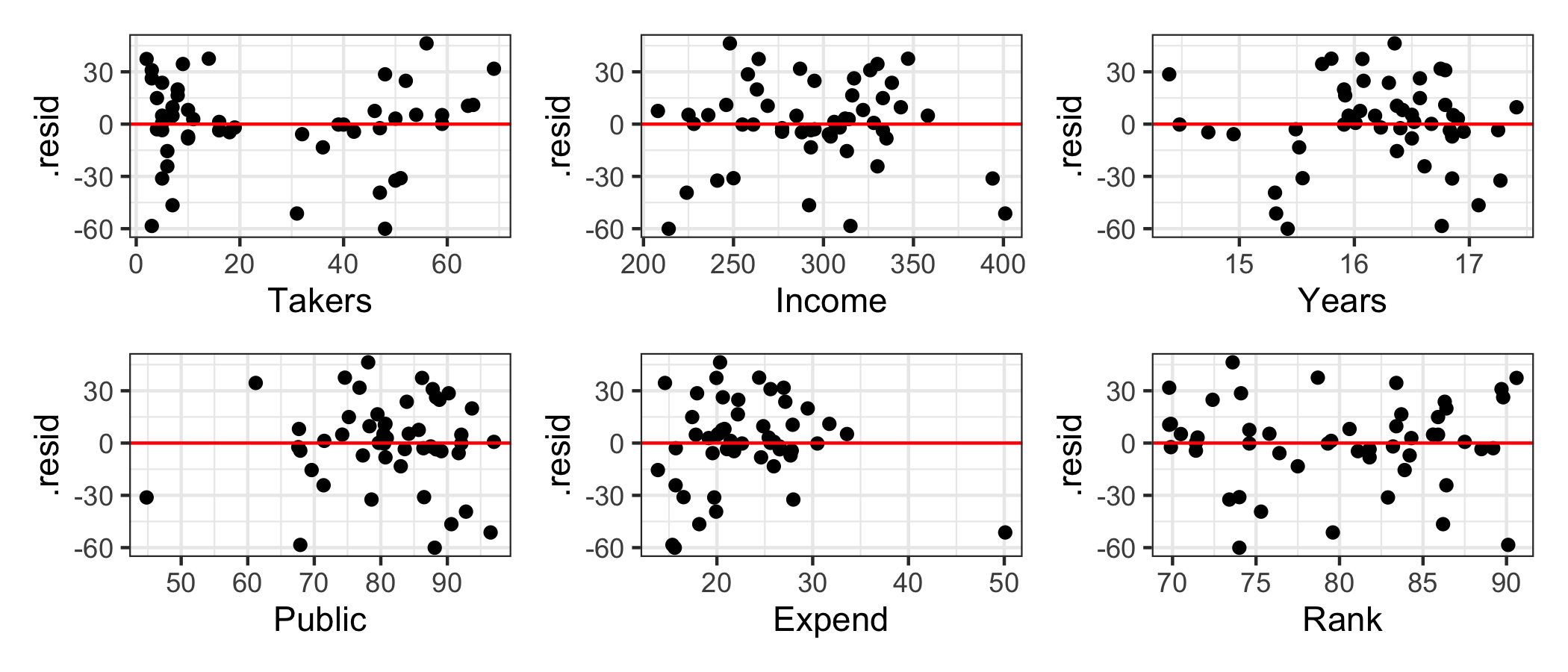
Linearity: Residuals vs. each predictor
If there is some pattern in the plot of residuals vs. predicted values, you can look at individual plots of residuals vs. each predictor to try to identify the issue.
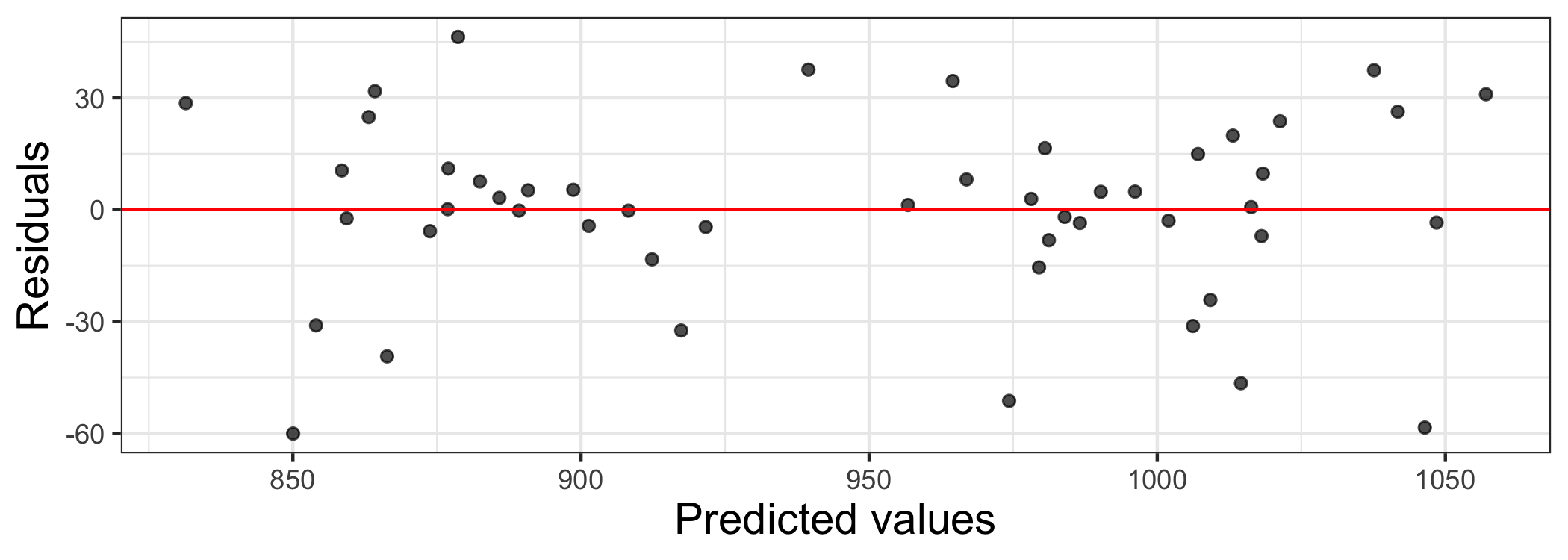
Checking linearity
✅ The plot of residuals vs. predicted shows no distinguishable pattern
✅ The plots of residuals vs. each predictor variable are generally fine; perhaps look into Years more closely.
The linearity condition is generally satisfied.
Checking constant variance
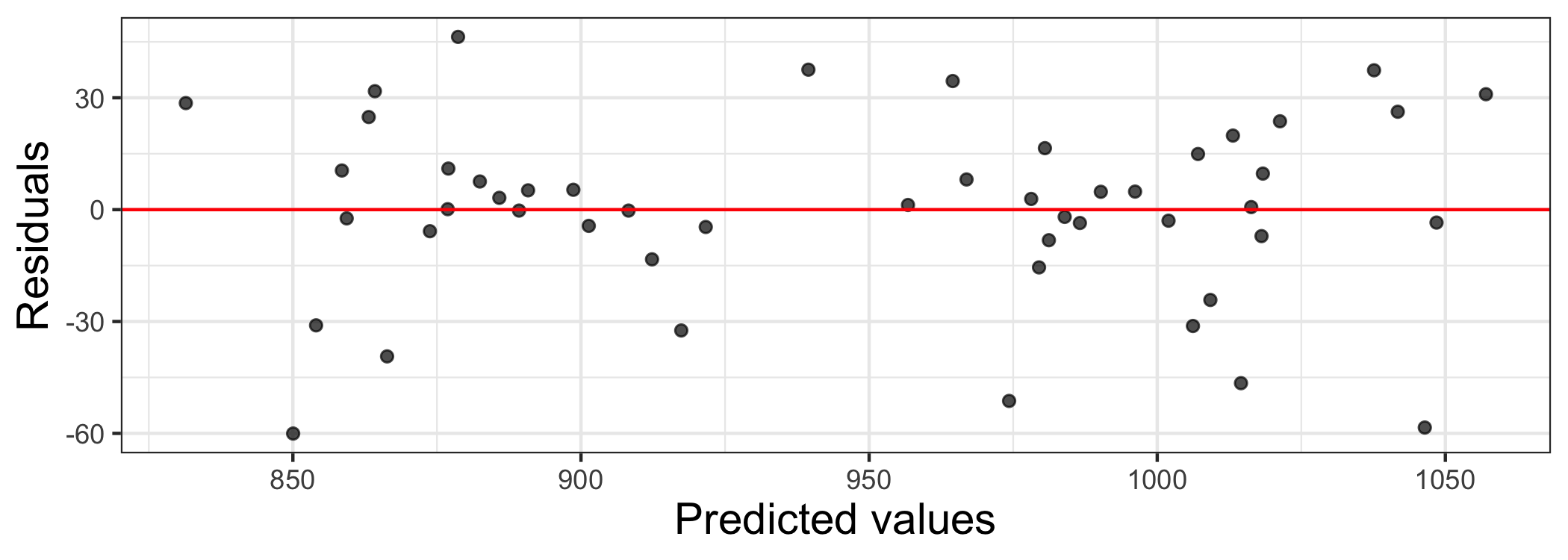
✅ The vertical spread of the residuals is relatively constant across the plot. The constant variance condition is satisfied.
Checking normality
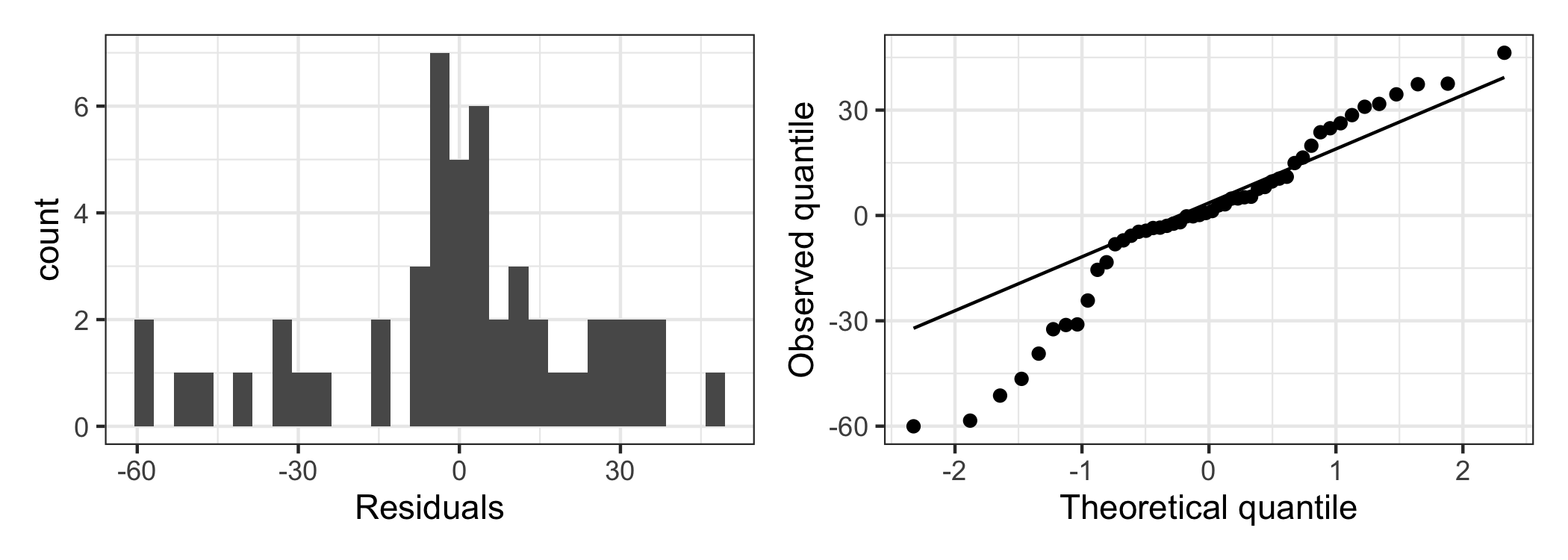
Checking normality

⚠️ Normality is not satisfied. However, \(n>30\), so by the Central Limit Theorem, we can still do inference about the model parameters.
Checking independence
We can often check the independence condition based on the context of the data and how the observations were collected.
If the data were collected in a particular order, examine a scatterplot of the residuals versus order in which the data were collected.
If there is a grouping variable lurking in the background, check the residuals based on that grouping variable.
Checking independence
Since the observations are US states, let's take a look at the residuals by region.
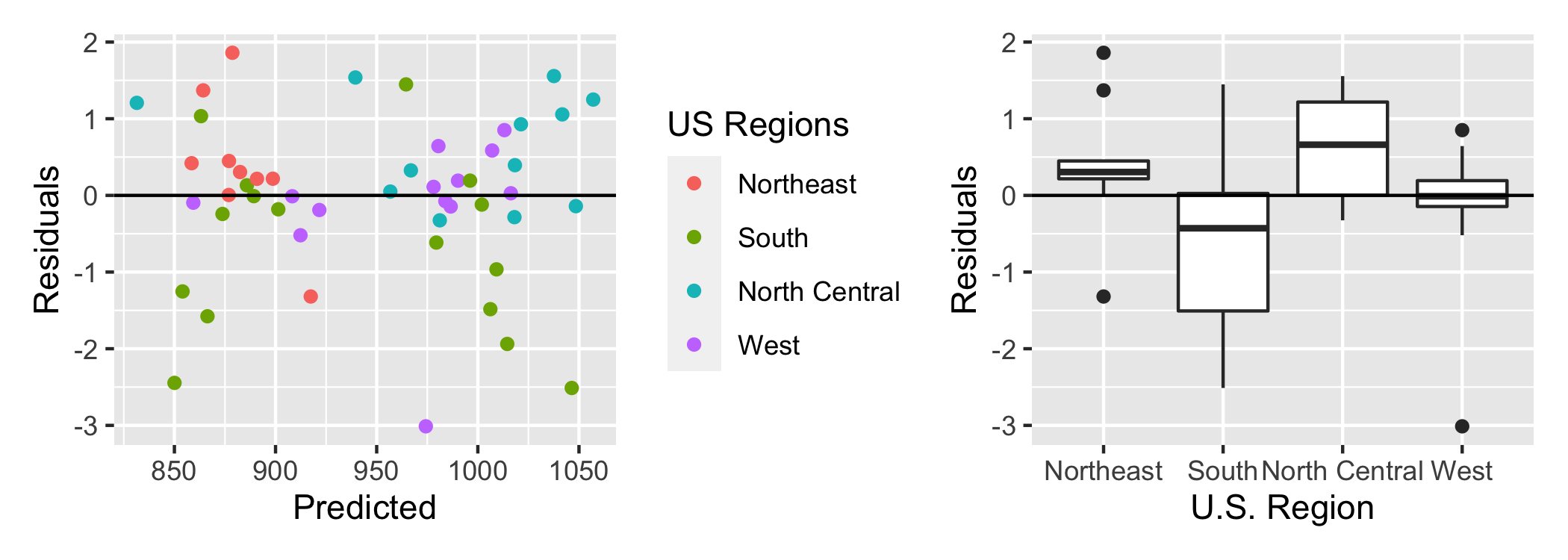
Checking independence
❌ The model tends to overpredict for states in the South and underpredict for states in the North Central, so the independence condition is not satisfied.
Multiple linear regression is not robust to violations of independence, so before moving forward, we should try fitting a model that includes region to account for these differences by region.