Logistic regression

class: center, middle, inverse, title-slide

# Logistic regression
## Inference
### Prof. Maria Tackett

---

class: middle, center

## [Click for PDF of slides](20-logistic-inference.pdf)

---

## Risk of coronary heart disease

.midi[This dataset is from an ongoing cardiovascular study on residents of the town of Framingham, Massachusetts. We want to examine the relationship between various health characteristics and the risk of having heart disease in the next 10 years.]

.midi[.vocab[`high_risk`]: 1 = High risk, 0 = Not high risk]

.midi[.vocab[`age`]: Age at exam time (in years)]

.midi[.vocab[`education`]: 1 = Some High School; 2 = High School or GED; 3 = Some College or Vocational School; 4 = College]

.midi[.vocab[`currentSmoker`]: 0 = nonsmoker; 1 = smoker]

---

## Modeling risk of coronary heart disease

|term        | estimate| std.error| statistic| p.value| conf.low| conf.high|
|:-----------|--------:|---------:|---------:|-------:|--------:|---------:|
|(Intercept) |   -5.385|     0.308|   -17.507|   0.000|   -5.995|    -4.788|
|age         |    0.073|     0.005|    13.385|   0.000|    0.063|     0.084|
|education2  |   -0.242|     0.112|    -2.162|   0.031|   -0.463|    -0.024|
|education3  |   -0.235|     0.134|    -1.761|   0.078|   -0.501|     0.023|
|education4  |   -0.020|     0.148|    -0.136|   0.892|   -0.317|     0.266|

`$$\small{\log\Big(\frac{\hat{\pi}}{1-\hat{\pi}}\Big) = -5.385 + 0.073 ~ \text{age} - 0.242 ~ \text{ed2} - 0.235 ~ \text{ed3} - 0.020 ~ \text{ed4}}$$`
---

## Hypothesis test for `\(\beta_j\)`

.vocab[Hypotheses]: `\(H_0: \beta_j = 0 \hspace{2mm} \text{ vs } \hspace{2mm} H_a: \beta_j \neq 0\)`

--

.vocab[Test Statistic]: `$$z = \frac{\hat{\beta}_j - 0}{SE_{\hat{\beta}_j}}$$`

--

.vocab[P-value]: `\(P(|Z| > |z|)\)`,

where `\(Z \sim N(0, 1)\)`, the Standard Normal distribution

---

## Confidence interval for `\(\beta_j\)`

We can calculate the .vocab[C% confidence interval] for `\(\beta_j\)` as the following:

.eq[
`$$\Large{\hat{\beta}_j \pm z^* SE_{\hat{\beta}_j}}$$`
where `\(z^*\)` is calculated from the `\(N(0,1)\)` distribution

]

--

This is an interval for the change in the log-odds for every one unit increase in `\(x_j\)`.

---

## Interpretation in terms of the odds

The change in **odds** for every one unit increase in `\(x_j\)`.

.eq[
`$$\Large{\exp\{\hat{\beta}_j \pm z^* SE_{\hat{\beta}_j}\}}$$`
]

--

.vocab[Interpretation]: We are `\(C\%\)` confident that for every one unit increase in `\(x_j\)`, the odds multiply by a factor of `\(\exp\{\hat{\beta}_j - z^* SE_{\hat{\beta}_j}\}\)` to `\(\exp\{\hat{\beta}_j + z^* SE_{\hat{\beta}_j}\}\)`, holding all else constant.

---

## Model

|term        | estimate| std.error| statistic| p.value| conf.low| conf.high|
|:-----------|--------:|---------:|---------:|-------:|--------:|---------:|
|(Intercept) |   -5.385|     0.308|   -17.507|   0.000|   -5.995|    -4.788|
|age         |    0.073|     0.005|    13.385|   0.000|    0.063|     0.084|
|education2  |   -0.242|     0.112|    -2.162|   0.031|   -0.463|    -0.024|
|education3  |   -0.235|     0.134|    -1.761|   0.078|   -0.501|     0.023|
|education4  |   -0.020|     0.148|    -0.136|   0.892|   -0.317|     0.266|

---

## Let's look at the coefficient for `age`

.midi[
<table>
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
   <th style="text-align:right;"> conf.low </th>
   <th style="text-align:right;"> conf.high </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> (Intercept) </td>
   <td style="text-align:right;"> -5.385 </td>
   <td style="text-align:right;"> 0.308 </td>
   <td style="text-align:right;"> -17.507 </td>
   <td style="text-align:right;"> 0.000 </td>
   <td style="text-align:right;"> -5.995 </td>
   <td style="text-align:right;"> -4.788 </td>
  </tr>
  <tr>
   <td style="text-align:left;background-color: #dce5b2 !important;"> age </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.073 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.005 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 13.385 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.000 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.063 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.084 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education2 </td>
   <td style="text-align:right;"> -0.242 </td>
   <td style="text-align:right;"> 0.112 </td>
   <td style="text-align:right;"> -2.162 </td>
   <td style="text-align:right;"> 0.031 </td>
   <td style="text-align:right;"> -0.463 </td>
   <td style="text-align:right;"> -0.024 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education3 </td>
   <td style="text-align:right;"> -0.235 </td>
   <td style="text-align:right;"> 0.134 </td>
   <td style="text-align:right;"> -1.761 </td>
   <td style="text-align:right;"> 0.078 </td>
   <td style="text-align:right;"> -0.501 </td>
   <td style="text-align:right;"> 0.023 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education4 </td>
   <td style="text-align:right;"> -0.020 </td>
   <td style="text-align:right;"> 0.148 </td>
   <td style="text-align:right;"> -0.136 </td>
   <td style="text-align:right;"> 0.892 </td>
   <td style="text-align:right;"> -0.317 </td>
   <td style="text-align:right;"> 0.266 </td>
  </tr>
</tbody>
</table>
]
--

.eq[
.vocab[Hypotheses]

`$$H_0: \beta_{1} = 0 \hspace{2mm} \text{ vs } \hspace{2mm} H_a: \beta_{1} \neq 0$$`
]

---

## Let's look at the coefficient for `age`

.midi[
<table>
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
   <th style="text-align:right;"> conf.low </th>
   <th style="text-align:right;"> conf.high </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> (Intercept) </td>
   <td style="text-align:right;"> -5.385 </td>
   <td style="text-align:right;"> 0.308 </td>
   <td style="text-align:right;"> -17.507 </td>
   <td style="text-align:right;"> 0.000 </td>
   <td style="text-align:right;"> -5.995 </td>
   <td style="text-align:right;"> -4.788 </td>
  </tr>
  <tr>
   <td style="text-align:left;background-color: #dce5b2 !important;"> age </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.073 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.005 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 13.385 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.000 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.063 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.084 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education2 </td>
   <td style="text-align:right;"> -0.242 </td>
   <td style="text-align:right;"> 0.112 </td>
   <td style="text-align:right;"> -2.162 </td>
   <td style="text-align:right;"> 0.031 </td>
   <td style="text-align:right;"> -0.463 </td>
   <td style="text-align:right;"> -0.024 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education3 </td>
   <td style="text-align:right;"> -0.235 </td>
   <td style="text-align:right;"> 0.134 </td>
   <td style="text-align:right;"> -1.761 </td>
   <td style="text-align:right;"> 0.078 </td>
   <td style="text-align:right;"> -0.501 </td>
   <td style="text-align:right;"> 0.023 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education4 </td>
   <td style="text-align:right;"> -0.020 </td>
   <td style="text-align:right;"> 0.148 </td>
   <td style="text-align:right;"> -0.136 </td>
   <td style="text-align:right;"> 0.892 </td>
   <td style="text-align:right;"> -0.317 </td>
   <td style="text-align:right;"> 0.266 </td>
  </tr>
</tbody>
</table>
]

.eq[
.vocab[Test statistic]

`$$z = \frac{0.0733 - 0}{0.00547} = 13.4$$`
]

---

## Let's look at the coefficient for `age`

.midi[
<table>
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
   <th style="text-align:right;"> conf.low </th>
   <th style="text-align:right;"> conf.high </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> (Intercept) </td>
   <td style="text-align:right;"> -5.385 </td>
   <td style="text-align:right;"> 0.308 </td>
   <td style="text-align:right;"> -17.507 </td>
   <td style="text-align:right;"> 0.000 </td>
   <td style="text-align:right;"> -5.995 </td>
   <td style="text-align:right;"> -4.788 </td>
  </tr>
  <tr>
   <td style="text-align:left;background-color: #dce5b2 !important;"> age </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.073 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.005 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 13.385 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.000 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.063 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.084 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education2 </td>
   <td style="text-align:right;"> -0.242 </td>
   <td style="text-align:right;"> 0.112 </td>
   <td style="text-align:right;"> -2.162 </td>
   <td style="text-align:right;"> 0.031 </td>
   <td style="text-align:right;"> -0.463 </td>
   <td style="text-align:right;"> -0.024 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education3 </td>
   <td style="text-align:right;"> -0.235 </td>
   <td style="text-align:right;"> 0.134 </td>
   <td style="text-align:right;"> -1.761 </td>
   <td style="text-align:right;"> 0.078 </td>
   <td style="text-align:right;"> -0.501 </td>
   <td style="text-align:right;"> 0.023 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education4 </td>
   <td style="text-align:right;"> -0.020 </td>
   <td style="text-align:right;"> 0.148 </td>
   <td style="text-align:right;"> -0.136 </td>
   <td style="text-align:right;"> 0.892 </td>
   <td style="text-align:right;"> -0.317 </td>
   <td style="text-align:right;"> 0.266 </td>
  </tr>
</tbody>
</table>
]

.eq[
.vocab[P-value]

`$$P(|Z| > |13.4|) \approx 0$$`
]

---

## Let's look at the coefficient for `age`

.midi[
<table>
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
   <th style="text-align:right;"> conf.low </th>
   <th style="text-align:right;"> conf.high </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> (Intercept) </td>
   <td style="text-align:right;"> -5.385 </td>
   <td style="text-align:right;"> 0.308 </td>
   <td style="text-align:right;"> -17.507 </td>
   <td style="text-align:right;"> 0.000 </td>
   <td style="text-align:right;"> -5.995 </td>
   <td style="text-align:right;"> -4.788 </td>
  </tr>
  <tr>
   <td style="text-align:left;background-color: #dce5b2 !important;"> age </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.073 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.005 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 13.385 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.000 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.063 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.084 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education2 </td>
   <td style="text-align:right;"> -0.242 </td>
   <td style="text-align:right;"> 0.112 </td>
   <td style="text-align:right;"> -2.162 </td>
   <td style="text-align:right;"> 0.031 </td>
   <td style="text-align:right;"> -0.463 </td>
   <td style="text-align:right;"> -0.024 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education3 </td>
   <td style="text-align:right;"> -0.235 </td>
   <td style="text-align:right;"> 0.134 </td>
   <td style="text-align:right;"> -1.761 </td>
   <td style="text-align:right;"> 0.078 </td>
   <td style="text-align:right;"> -0.501 </td>
   <td style="text-align:right;"> 0.023 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education4 </td>
   <td style="text-align:right;"> -0.020 </td>
   <td style="text-align:right;"> 0.148 </td>
   <td style="text-align:right;"> -0.136 </td>
   <td style="text-align:right;"> 0.892 </td>
   <td style="text-align:right;"> -0.317 </td>
   <td style="text-align:right;"> 0.266 </td>
  </tr>
</tbody>
</table>
]

```r
2 * pnorm(13.4,lower.tail = FALSE)
```

```
## [1] 6.046315e-41
```

---

## Let's look at the coefficient for `age`

.midi[
<table>
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
   <th style="text-align:right;"> conf.low </th>
   <th style="text-align:right;"> conf.high </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> (Intercept) </td>
   <td style="text-align:right;"> -5.385 </td>
   <td style="text-align:right;"> 0.308 </td>
   <td style="text-align:right;"> -17.507 </td>
   <td style="text-align:right;"> 0.000 </td>
   <td style="text-align:right;"> -5.995 </td>
   <td style="text-align:right;"> -4.788 </td>
  </tr>
  <tr>
   <td style="text-align:left;background-color: #dce5b2 !important;"> age </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.073 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.005 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 13.385 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.000 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.063 </td>
   <td style="text-align:right;background-color: #dce5b2 !important;"> 0.084 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education2 </td>
   <td style="text-align:right;"> -0.242 </td>
   <td style="text-align:right;"> 0.112 </td>
   <td style="text-align:right;"> -2.162 </td>
   <td style="text-align:right;"> 0.031 </td>
   <td style="text-align:right;"> -0.463 </td>
   <td style="text-align:right;"> -0.024 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education3 </td>
   <td style="text-align:right;"> -0.235 </td>
   <td style="text-align:right;"> 0.134 </td>
   <td style="text-align:right;"> -1.761 </td>
   <td style="text-align:right;"> 0.078 </td>
   <td style="text-align:right;"> -0.501 </td>
   <td style="text-align:right;"> 0.023 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> education4 </td>
   <td style="text-align:right;"> -0.020 </td>
   <td style="text-align:right;"> 0.148 </td>
   <td style="text-align:right;"> -0.136 </td>
   <td style="text-align:right;"> 0.892 </td>
   <td style="text-align:right;"> -0.317 </td>
   <td style="text-align:right;"> 0.266 </td>
  </tr>
</tbody>
</table>
]

.vocab[Conclusion]: The p-value is very small, so we reject `\(H_0\)`. The data provide sufficient evidence that age is a statistically significant predictor of whether someone is high risk of having heart disease, *after accounting for education*.

---

class: middle, center

## Comparing models

---

## Log likelihood

.eq[
`$$\log L = \sum\limits_{i=1}^n[y_i \log(\hat{\pi}_i) + (1 - y_i)\log(1 - \hat{\pi}_i)]$$`
]

--

- Measure of how well the model fits the data

--

- Higher values of `\(\log L\)` are better

--

- .vocab[Deviance] = `\(-2 \log L\)`
  - `\(-2 \log L\)` follows a `\(\chi^2\)` distribution with `\(n - p - 1\)` degrees of freedom
  
---

## Comparing nested models

- Suppose there are two models: 
    - Reduced Model includes predictors `\(x_1, \ldots, x_q\)`
    - Full Model includes predictors `\(x_1, \ldots, x_q, x_{q+1}, \ldots, x_p\)`

--

- We want to test the hypotheses
`$$\begin{aligned}&H_0: \beta_{q+1} = \dots = \beta_p = 0 \\
& H_a: \text{ at least 1 }\beta_j \text{ is not } 0\end{aligned}$$`

--

- To do so, we will use the .vocab[Drop-in-deviance test] (also known as the Nested Likelihood Ratio test)

---

## Drop-in-deviance test

.vocab[Hypotheses]:
`$$\begin{aligned}&H_0: \beta_{q+1} = \dots = \beta_p = 0 \\
& H_a: \text{ at least 1 }\beta_j \text{ is not } 0\end{aligned}$$`

--

.vocab[Test Statistic]: `$$G = (-2 \log L_{reduced}) - (-2 \log L_{full})$$`

--

.vocab[P-value]: `\(P(\chi^2 > G)\)`,

calculated using a `\(\chi^2\)` distribution with degrees of freedom equal to the difference in the number of parameters in the full and reduced models

---

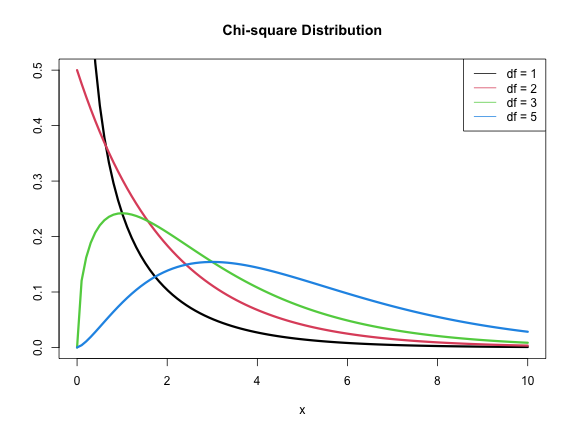
## `\(\chi^2\)` distribution

<img src="20-logistic-inference_files/figure-html/unnamed-chunk-11-1.png" style="display: block; margin: auto;" />

---

.small[

]

|term        | estimate| std.error| statistic| p.value| conf.low| conf.high|
|:-----------|--------:|---------:|---------:|-------:|--------:|---------:|
|(Intercept) |   -5.385|     0.308|   -17.507|   0.000|   -5.995|    -4.788|
|age         |    0.073|     0.005|    13.385|   0.000|    0.063|     0.084|
|education2  |   -0.242|     0.112|    -2.162|   0.031|   -0.463|    -0.024|
|education3  |   -0.235|     0.134|    -1.761|   0.078|   -0.501|     0.023|
|education4  |   -0.020|     0.148|    -0.136|   0.892|   -0.317|     0.266|

<br>

--

.question[
Should we add `currentSmoker` to this model?
]

---

## Should we add `currentSmoker` to the model?

```r
model_reduced <- glm(high_risk ~ age + education, 
              data = heart, family = "binomial")
```

```r
model_full <- glm(high_risk ~ age + education + 
*                   currentSmoker,
              data = heart, family = "binomial")
```

---

## Should we add `currentSmoker` to the model?

```r
# Calculate deviance for each model
(dev_reduced <- glance(model_reduced)$deviance)
```

```
## [1] 3300.135
```

```r
(dev_full <- glance(model_full)$deviance)
```

```
## [1] 3279.359
```

--

```r
# Drop-in-deviance test statistic
(test_stat <- dev_reduced - dev_full)
```

```
## [1] 20.77589
```

---

## Should we add `currentSmoker` to the model?

```r
# p-value
#1 = number of new model terms in model 2
pchisq(test_stat, 1, lower.tail = FALSE) 
```

```
## [1] 5.162887e-06
```

--

.vocab[Conclusion]: The p-value is very small, so we reject `\(H_0\)`. The data provide sufficient evidence that the coefficient of `currentSmoker` is not equal to 0. Therefore, we should add it to the model.

---

## Drop-in-Deviance test in R

We can use the **`anova`** function to conduct this test

- Add **`test = "Chisq"`** to conduct the drop-in-deviance test

```r
anova(model_reduced, model_full, test = "Chisq") %>%
  tidy()
```

```
## # A tibble: 2 x 5
##   Resid..Df Resid..Dev    df Deviance     p.value
##       <dbl>      <dbl> <dbl>    <dbl>       <dbl>
## 1      4130      3300.    NA     NA   NA         
## 2      4129      3279.     1     20.8  0.00000516
```

---

## Model selection

Use AIC or BIC for model selection

.eq[
`$$\begin{align}&AIC = - 2 * \log L - \color{red}{n\log(n)}+ 2(p +1)\\[5pt]
&BIC =- 2 * \log L - \color{red}{n\log(n)} + log(n)\times(p+1)\end{align}$$`
]

---

## AIC from `glance` function

Let's look at the AIC for the model that includes `age`, `education`, and `currentSmoker`

```r
glance(model_full)$AIC
```

```
## [1] 3291.359
```

--

**Calculating AIC**

```r
- 2 * glance(model_full)$logLik + 2 * (5 + 1)
```

```
## [1] 3291.359
```

---

## Comparing the models using AIC

Let's compare the full and reduced models using AIC.

```r
glance(model_reduced)$AIC
```

```
## [1] 3310.135
```

```r
glance(model_full)$AIC
```

```
## [1] 3291.359
```

.question[
Based on AIC, which model would you choose?
]

---

## Comparing the models using BIC

Let's compare the full and reduced models using BIC

```r
glance(model_reduced)$BIC
```

```
## [1] 3341.772
```

```r
glance(model_full)$BIC
```

```
## [1] 3329.323
```

.question[
Based on BIC, which model would you choose?
]