class: center, middle, inverse, title-slide # Multiple linear regression ### Prof. Maria Tackett --- class: middle, center ## [Click here for PDF of slides](10-mlr-intro.pdf) --- ## Topics - Introduce multiple linear regression - Interpret a coefficient `\(\hat{\beta}_j\)` - Use the model to calculate predicted values and the corresponding interval --- ## House prices in Levittown The data set contains the sales price and characteristics of 85 homes in Levittown, NY that sold between June 2010 and May 2011. Levittown was built right after WWII and was the first planned suburban community built using mass production techniques. The article ["Levittown, the prototypical American suburb – a history of cities in 50 buildings, day 25"](https://www.theguardian.com/cities/2015/apr/28/levittown-america-prototypical-suburb-history-cities) gives an overview of Levittown's controversial history. --- ## Analysis goals We would like to use the characteristics of a house to understand variability in the sales price. To do so, we will fit a .vocab[multiple linear regression model] Using our model, we can answers questions such as - What is the relationship between the characteristics of a house in Levittown and its sale price? - Given its characteristics, what is the expected sale price of a house in Levittown? --- ## The data .midi[ ``` ## # A tibble: 10 x 7 ## bedrooms bathrooms living_area lot_size year_built property_tax sale_price ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 4 1 1380 6000 1948 8360 350000 ## 2 4 2 1761 7400 1951 5754 360000 ## 3 4 2 1564 6000 1948 8982 350000 ## 4 5 2 2904 9898 1949 11664 375000 ## 5 5 2.5 1942 7788 1948 8120 370000 ## 6 4 2 1830 6000 1948 8197 335000 ## 7 4 1 1585 6000 1948 6223 295000 ## 8 4 1 941 6800 1951 2448 250000 ## 9 4 1.5 1481 6000 1948 9087 299990 ## 10 3 2 1630 5998 1948 9430 375000 ``` ] --- ## Variables **Predictors** - .vocab[`bedrooms`]: Number of bedrooms - .vocab[`bathrooms`]: Number of bathrooms - .vocab[`living_area`]: Total living area of the house (in square feet) - .vocab[`lot_size`]: Total area of the lot (in square feet) - .vocab[`year_built`]: Year the house was built - .vocab[`property_tax`]: Annual property taxes (in U.S. dollars) **Response** - .vocab[`sale_price`]: Sales price (in U.S. 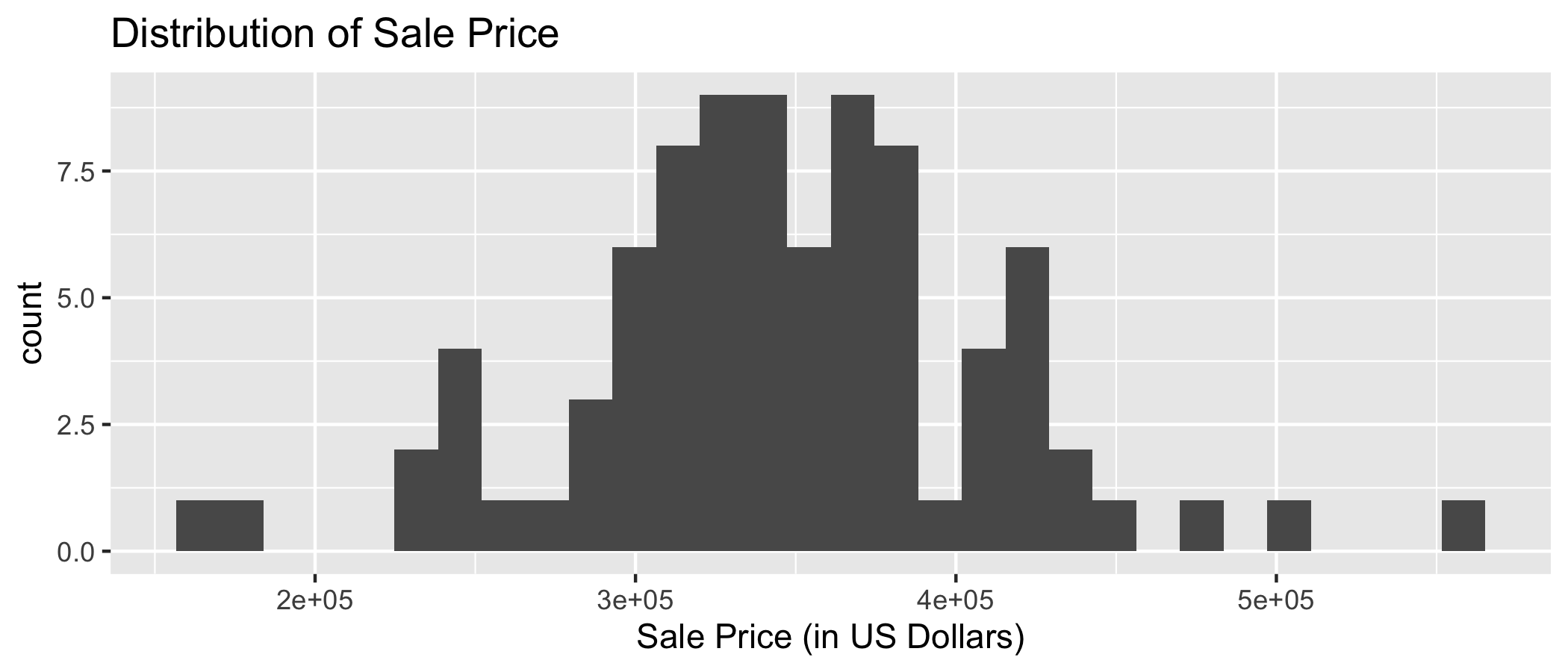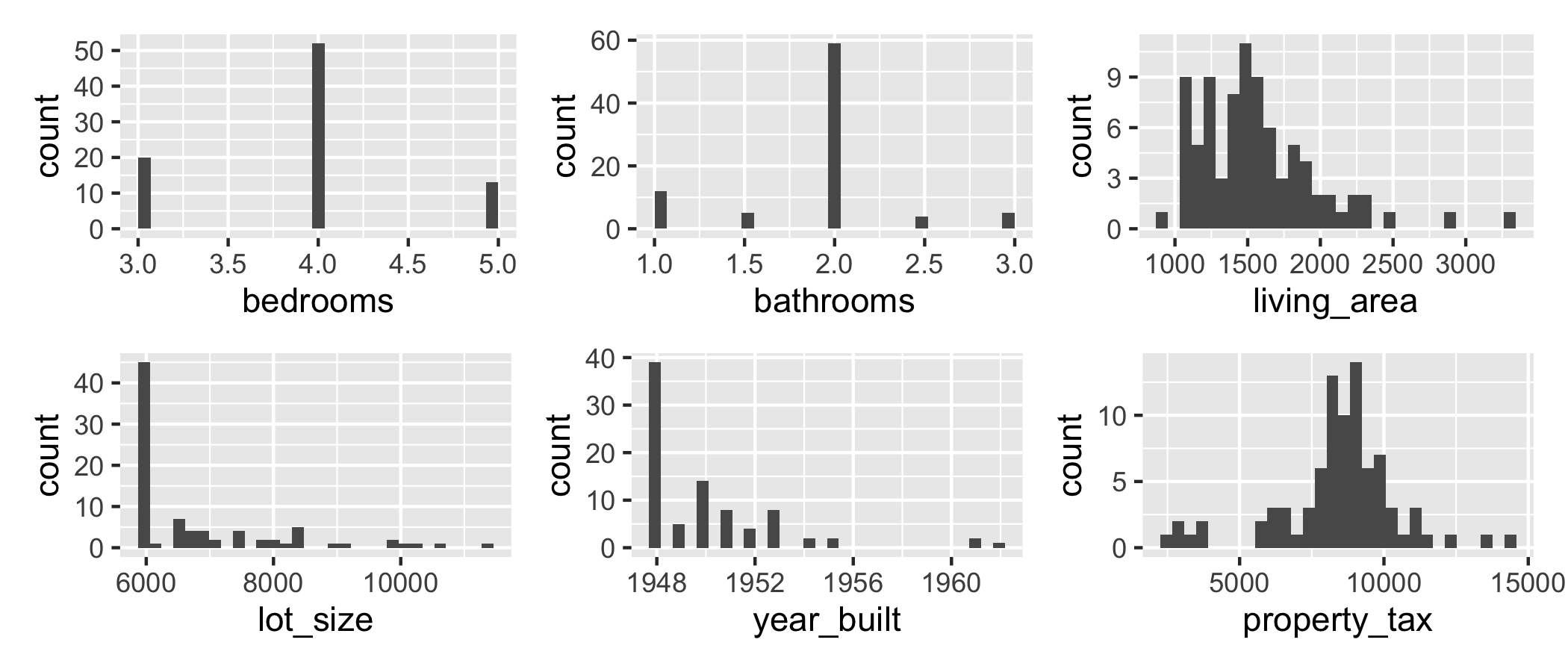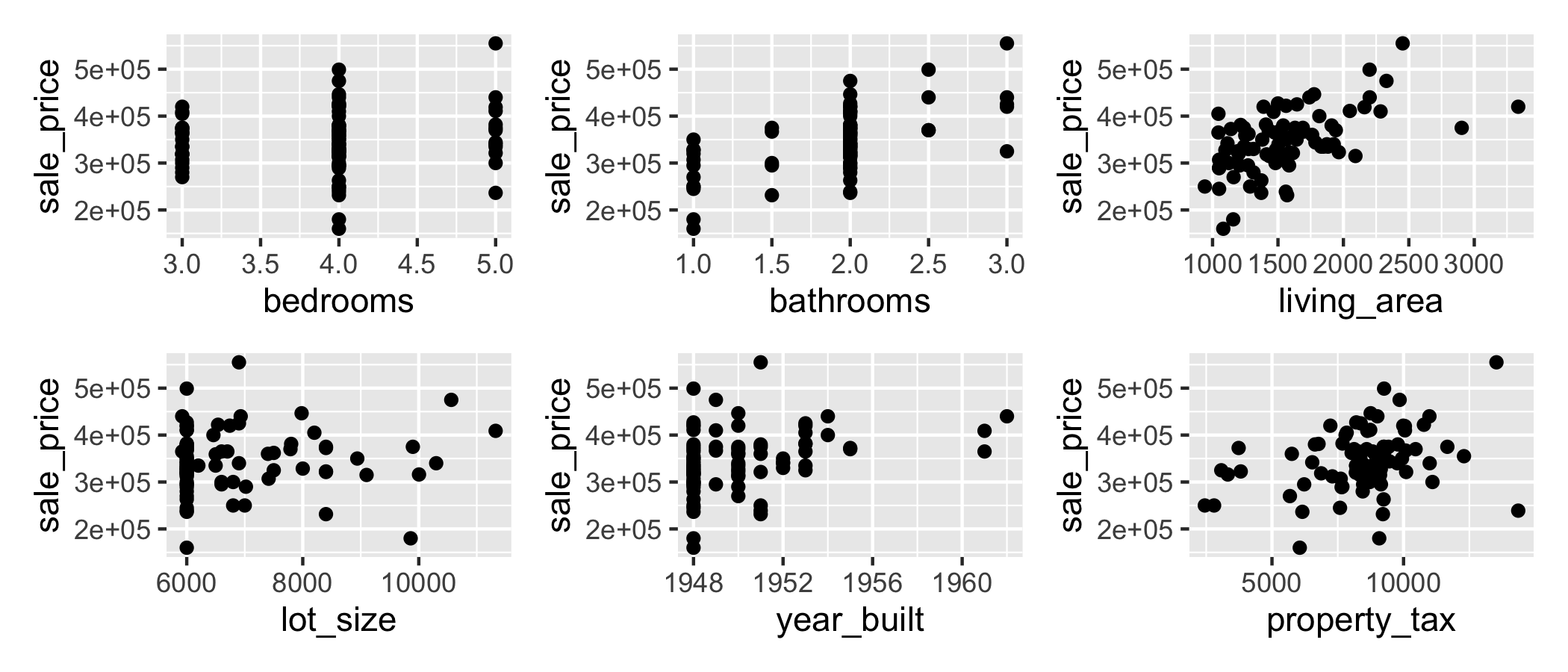dollars) --- ## EDA: Response variable <img src="10-mlr-intro_files/figure-html/unnamed-chunk-5-1.png" style="display: block; margin: auto;" /> --- ## EDA: Predictor variables <img src="10-mlr-intro_files/figure-html/unnamed-chunk-6-1.png" style="display: block; margin: auto;" /> --- ## EDA: Response vs. Predictors <img src="10-mlr-intro_files/figure-html/unnamed-chunk-7-1.png" style="display: block; margin: auto;" /> --- class: middle So far we've used a .vocab[*single predictor variable*] to understand variation in a quantitative response variable -- Now we want to use .vocab[*multiple predictor variables*] to understand variation in a quantitative response variable --- ## Multiple linear regression (MLR) Based on the analysis goals, we will use a .vocab[multiple linear regression] model of the following form .eq[ .small[ `$$\begin{aligned}\hat{\text{sale_price}} ~ = & ~ \hat{\beta}_0 + \hat{\beta}_1 \text{bedrooms} + \hat{\beta}_2 \text{bathrooms} + \hat{\beta}_3 \text{living_area} \\ &+ \hat{\beta}_4 \text{lot_size} + \hat{\beta}_5 \text{year_built} + \hat{\beta}_6 \text{property_tax}\end{aligned}$$` ] ] Similar to simple linear regression, this model assumes that at each combination of the predictor variables, the values **`sale_price`** follow a Normal distribution --- ## Regression Model - **Recall:** The simple linear regression model assumes `$$Y|X\sim N(\beta_0 + \beta_1 X, \sigma_{\epsilon}^2)$$` -- <br> - **Similarly:** The multiple linear regression model assumes `$$Y|X_1, X_2, \ldots, X_p \sim N(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_p X_p, \sigma_{\epsilon}^2)$$` --- class: middle, center .eq[ For a given observation `\((x_{i1}, x_{i2} \ldots, x_{ip}, y_i)\)` `$$y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_p x_{ip} + \epsilon_{i} \hspace{8mm} \epsilon_i \sim N(0,\sigma_\epsilon^2)$$` ] --- ## Regression Model - At any combination of the predictors, the mean value of the response `\(Y\)`, is `$$\mu_{Y|X_1, \ldots, X_p} = \beta_0 + \beta_1 X_{1} + \beta_2 X_2 + \dots + \beta_p X_p$$` -- <br> - Using multiple linear regression, we can estimate the mean response for any combination of predictors `$$\hat{Y} = \hat{\beta}_0 + \hat{\beta}_1 X_{1} + \hat{\beta}_2 X_2 + \dots + \hat{\beta}_p X_{p}$$` --- ## Home price model .small[ |term | estimate| std.error| statistic| p.value| |:------------|------------:|-----------:|---------:|-------:| |(Intercept) | -7148818.957| 3820093.694| -1.871| 0.065| |bedrooms | -12291.011| 9346.727| -1.315| 0.192| |bathrooms | 51699.236| 13094.170| 3.948| 0.000| |living_area | 65.903| 15.979| 4.124| 0.000| |lot_size | -0.897| 4.194| -0.214| 0.831| |year_built | 3760.898| 1962.504| 1.916| 0.059| |property_tax | 1.476| 2.832| 0.521| 0.604| ] --- class: middle .eq[ `$$\begin{align}\hat{\text{price}} = & -7148818.957 - 12291.011 \times \text{bedrooms}\\[5pt] &+ 51699.236 \times \text{bathrooms} + 65.903 \times \text{living area}\\[5pt] &- 0.897 \times \text{lot size} + 3760.898 \times \text{year built}\\[5pt] &+ 1.476 \times \text{property tax}\end{align}$$` ] --- ## Interpreting `\(\hat{\beta}_j\)` - The estimated coefficient `\(\hat{\beta}_j\)` is the expected change in the mean of `\(y\)` when `\(x_j\)` increases by one unit, **<i>holding the values of all other predictor variables constant</i>**. -- <br> - **Example:** The estimated coefficient for **`living_area`** is 65.90. This means for each additional square foot of living area, we expect the sale price of a house in Levittown, NY to increase by $65.90, on average, holding all other predictor variables constant. --- ## Prediction **Example:** What is the predicted sale price for a house in Levittown, NY with 3 bedrooms, 1 bathroom, 1050 square feet of living area, 6000 square foot lot size, built in 1948 with $6306 in property taxes? .midi[ ```r -7148818.957 - 12291.011 * 3 + 51699.236 * 1 + 65.903 * 1050 - 0.897 * 6000 + 3760.898 * 1948 + 1.476 * 6306 ``` ``` ## [1] 265360.4 ``` ] -- The predicted sale price for a house in Levittown, NY with 3 bedrooms, 1 bathroom, 1050 square feet of living area, 6000 square foot lot size, built in 1948 with $6306 in property taxes is **$265,360**. --- ## Intervals for predictions Just like with simple linear regression, we can use the .vocab[`predict`] function in R to calculate the appropriate intervals for our predicted values ```r x0 <- data.frame(bedrooms = 3, bathrooms = 1, living_area = 1050, lot_size = 6000, year_built = 1948, property_tax = 6306) ``` --- ## Confidence interval for `\(\hat{\mu}_y\)` Calculate a 95% confidence interval for the **estimated mean price** of houses in Levittown, NY with 3 bedrooms, 1 bathroom, 1050 square feet of living area, 6000 square foot lot size, built in 1948 with $6306 in property taxes: ```r predict(price_model, x0, interval = "confidence", level = 0.95) ``` ``` ## fit lwr upr ## 1 265360.2 238481.7 292238.7 ``` --- ## Prediction interval for `\(\hat{y}\)` Calculate a 95% prediction interval for an individual house in Levittown, NY with 3 bedrooms, 1 bathroom, 1050 square feet of living area, 6000 square foot lot size, built in 1948 with $6306 in property taxes: ```r predict(price_model, x0, interval = "prediction", level = 0.95) ``` ``` ## fit lwr upr ## 1 265360.2 167276.8 363443.6 ``` --- ## 🛑 Cautions - .vocab3[Do not extrapolate!] Because there are multiple predictor variables, there is the potential to extrapolate in many directions -- - The multiple regression model only shows .vocab3[association, not causality] + To show causality, you must have a carefully designed experiment or carefully account for confounding variables in an observational study --- ## Recap - Introduced multiple linear regression - Interpreted a coefficient `\(\hat{\beta}_j\)` - Used the model to calculate predicted values and the corresponding interval