Model diagnostics
Prof. Maria Tackett
Topics
Identifying influential points
- Leverage
- Standardized residuals
- Cook's Distance
Multicollinearity
Influential points
Influential Point
An observation is influential if removing it substantially changes the coefficients of the regression model
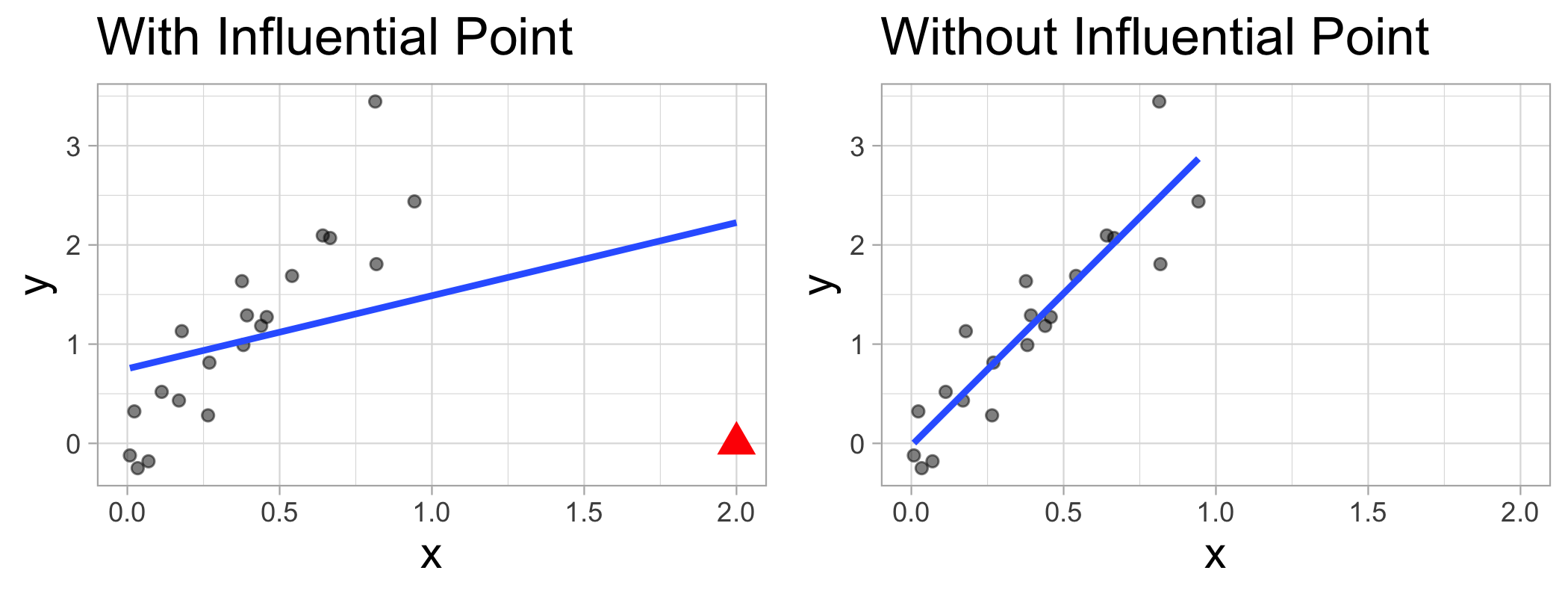
Influential points
- Influential points have a large impact on the coefficients and standard errors used for inference
Influential points
Influential points have a large impact on the coefficients and standard errors used for inference
These points can sometimes be identified in a scatterplot if there is only one predictor variable
- This is often not the case when there are multiple predictors
Influential points
Influential points have a large impact on the coefficients and standard errors used for inference
These points can sometimes be identified in a scatterplot if there is only one predictor variable
- This is often not the case when there are multiple predictors
We will use measures to quantify an individual observation's influence on the regression model
- leverage, standardized residuals, and Cook's distance
Model diagnostics in R
Use the augment function in the broom package to output the model diagnostics (along with the predicted values and residuals)
- response and predictor variables in the model
.fitted: predicted values.se.fit: standard errors of predicted values.resid: residuals.hat: leverage.sigma: estimate of residual standard deviation when the corresponding observation is dropped from model.cooksd: Cook's distance.std.resid: standardized residuals]
Example: SAT Averages by State
This data set contains the average SAT score (out of 1600) and other variables that may be associated with SAT performance for each of the 50 U.S. states. The data is based on test takers for the 1982 exam.
Response variable:
SAT: average total SAT score
Data comes from case1201 data set in the Sleuth3 package
SAT Averages: Predictors
Takers: percentage of high school seniors who took examIncome: median income of families of test-takers ($ hundreds)Years: average number of years test-takers had formal education in social sciences, natural sciences, and humanitiesPublic: percentage of test-takers who attended public high schoolsExpend: total state expenditure on high schools ($ hundreds per student)Rank: median percentile rank of test-takers within their high school classes
Model
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -94.659 | 211.510 | -0.448 | 0.657 |
| Takers | -0.480 | 0.694 | -0.692 | 0.493 |
| Income | -0.008 | 0.152 | -0.054 | 0.957 |
| Years | 22.610 | 6.315 | 3.581 | 0.001 |
| Public | -0.464 | 0.579 | -0.802 | 0.427 |
| Expend | 2.212 | 0.846 | 2.615 | 0.012 |
| Rank | 8.476 | 2.108 | 4.021 | 0.000 |
SAT: Augmented Data
## Rows: 50## Columns: 14## $ SAT <int> 1088, 1075, 1068, 1045, 1045, 1033, 1028, 1022, 1017, 1011,…## $ Takers <int> 3, 2, 3, 5, 5, 8, 7, 4, 5, 10, 5, 4, 9, 8, 7, 3, 6, 16, 19,…## $ Income <int> 326, 264, 317, 338, 293, 263, 343, 333, 328, 304, 358, 295,…## $ Years <dbl> 16.79, 16.07, 16.57, 16.30, 17.25, 15.91, 17.41, 16.57, 16.…## $ Public <dbl> 87.8, 86.2, 88.3, 83.9, 83.6, 93.7, 78.3, 75.2, 97.0, 77.3,…## $ Expend <dbl> 25.60, 19.95, 20.62, 27.14, 21.05, 29.48, 24.84, 17.42, 25.…## $ Rank <dbl> 89.7, 90.6, 89.8, 86.3, 88.5, 86.4, 83.4, 85.9, 87.5, 84.2,…## $ .fitted <dbl> 1057.0438, 1037.6261, 1041.7431, 1021.3039, 1048.4680, 1013…## $ .resid <dbl> 30.9562319, 37.3739084, 26.2569334, 23.6961288, -3.4680381,…## $ .hat <dbl> 0.11609974, 0.16926150, 0.11000956, 0.06036139, 0.12261873,…## $ .sigma <dbl> 26.16716, 25.89402, 26.30760, 26.38760, 26.64972, 26.43025,…## $ .cooksd <dbl> 2.931280e-02, 7.051849e-02, 1.970989e-02, 7.901850e-03, 3.9…## $ .std.resid <dbl> 1.24986670, 1.55651598, 1.05649773, 0.92792786, -0.14054225…## $ obs_num <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …Leverage
Leverage
- Leverage: measure of the distance between an observation's values of the predictor variables and the average values of the predictor variables for the entire data set
Leverage
Leverage: measure of the distance between an observation's values of the predictor variables and the average values of the predictor variables for the entire data set
An observation has high leverage if its combination of values for the predictor variables is very far from the typical combination of values in the data
Leverage
Leverage: measure of the distance between an observation's values of the predictor variables and the average values of the predictor variables for the entire data set
An observation has high leverage if its combination of values for the predictor variables is very far from the typical combination of values in the data
Observations with high leverage should be considered as potential influential points
Calculating leverage
Simple Regression: leverage of the ith observation
hi=1n+(xi−ˉx)2∑nj=1(xj−ˉx)2
Calculating leverage
Simple Regression: leverage of the ith observation
hi=1n+(xi−ˉx)2∑nj=1(xj−ˉx)2
Multiple Regression: leverage of the ith observation is the ith diagonal of H=X(XTX)−1XT
Calculating leverage
Simple Regression: leverage of the ith observation
hi=1n+(xi−ˉx)2∑nj=1(xj−ˉx)2
Multiple Regression: leverage of the ith observation is the ith diagonal of H=X(XTX)−1XT
- Note: Leverage only depends on values of the predictor variables
High Leverage
The sum of the leverages for all points is p+1
- In the case of SLR ∑ni=1hi=2
High Leverage
The sum of the leverages for all points is p+1
In the case of SLR ∑ni=1hi=2
The "typical" leverage is (p+1)n
High Leverage
The sum of the leverages for all points is p+1
In the case of SLR ∑ni=1hi=2
The "typical" leverage is (p+1)n
An observation has high leverage if hi>2(p+1)n
High Leverage
If there is point with high leverage, ask
❓ Is there a data entry error?
❓ Is this observation within the scope of individuals for which you want to make predictions and draw conclusions?
❓ Is this observation impacting the estimates of the model coefficients, especially for interactions?
High Leverage
If there is point with high leverage, ask
❓ Is there a data entry error?
❓ Is this observation within the scope of individuals for which you want to make predictions and draw conclusions?
❓ Is this observation impacting the estimates of the model coefficients, especially for interactions?
Just because a point has high leverage does not necessarily mean it will have a substantial impact on the regression. Therefore we need to check other measures.
SAT: Leverage
High leverage if hi>2∗(6+1)50=0.28
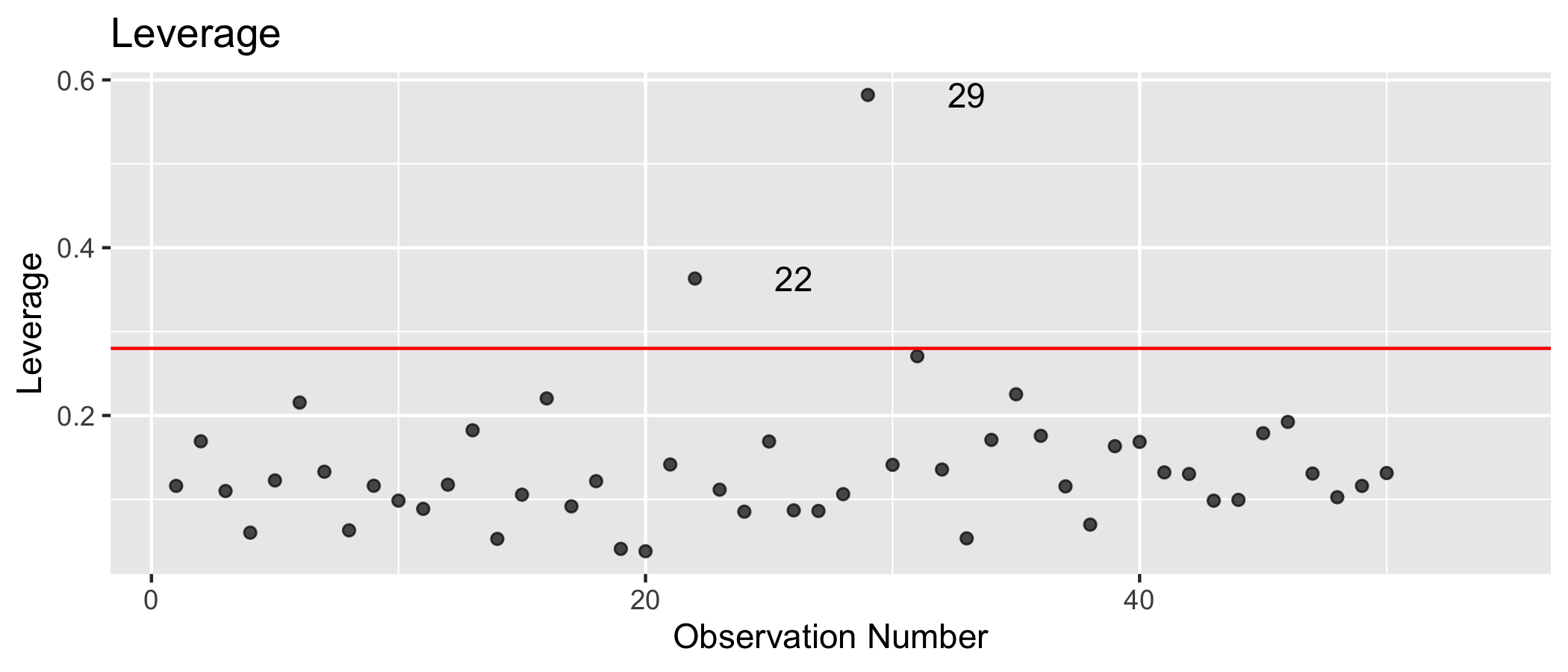
Observations with high leverage
| obs_num | Takers | Income | Years | Public | Expend | Rank |
|---|---|---|---|---|---|---|
| 22 | 5 | 394 | 16.85 | 44.8 | 19.72 | 82.9 |
| 29 | 31 | 401 | 15.32 | 96.5 | 50.10 | 79.6 |
Why do you think these observations have high leverage?
Let's dig into the data
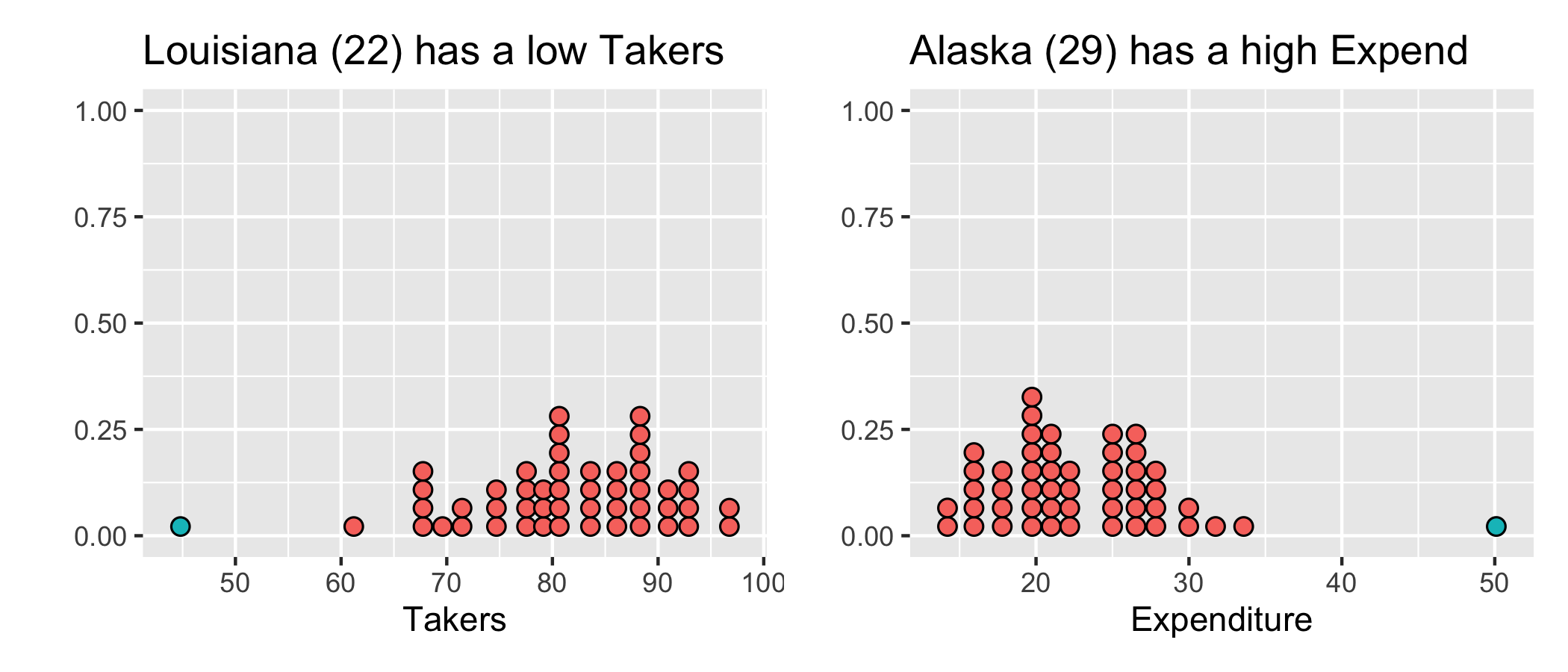
Standardized & Studentized Residuals
Standardized & Studentized Residuals
- What is the best way to identify outliers (points that don't fit the pattern from the regression line)?
Standardized & Studentized Residuals
What is the best way to identify outliers (points that don't fit the pattern from the regression line)?
Look for points that have large residuals
Standardized & Studentized Residuals
What is the best way to identify outliers (points that don't fit the pattern from the regression line)?
Look for points that have large residuals
We want a common scale, so we can more easily identify "large" residuals
Standardized & Studentized Residuals
What is the best way to identify outliers (points that don't fit the pattern from the regression line)?
Look for points that have large residuals
We want a common scale, so we can more easily identify "large" residuals
We will look at each residual divided by its standard error
Standardized & Studentized residuals
Standardized & Studentized residuals
std.resi=yi−ˆyiˆσϵ√1−hi
where ˆσϵ is the regression standard error
Standardized & Studentized residuals
std.resi=yi−ˆyiˆσϵ√1−hi
where ˆσϵ is the regression standard error
stud.resi=yi−ˆyiˆσ(i)√1−hi
Standardized & Studentized residuals
- Observations with high leverage tend to have low values of standardized residuals because they pull the regression line towards them
Standardized & Studentized residuals
Observations with high leverage tend to have low values of standardized residuals because they pull the regression line towards them
This issue is avoided using the studentized residuals, since the regression standard error is calculated without the possible influential point.
Standardized & Studentized residuals
Observations with high leverage tend to have low values of standardized residuals because they pull the regression line towards them
This issue is avoided using the studentized residuals, since the regression standard error is calculated without the possible influential point.
Standardized residuals are produced by
augmentin the column.std.resid
Standardized & Studentized residuals
Observations with high leverage tend to have low values of standardized residuals because they pull the regression line towards them
This issue is avoided using the studentized residuals, since the regression standard error is calculated without the possible influential point.
Standardized residuals are produced by
augmentin the column.std.residStudentized residuals can be calculated using
.sigma,.resid, and.hatproduced byaugment
Using standardized & studentized residuals
Observations that have standardized residuals of large magnitude are outliers, since they don't fit the pattern determined by the regression model
An observation is a moderate outlier if its standardized residual is beyond ±2.
An observation is a serious outlier if its standardized residual is beyond ±3.
Using standardized & studentized residuals
Observations that have standardized residuals of large magnitude are outliers, since they don't fit the pattern determined by the regression model
An observation is a moderate outlier if its standardized residual is beyond ±2.
An observation is a serious outlier if its standardized residual is beyond ±3.
Make residual plots with standardized residuals to make it easier to identify outliers and check constant variance condition.
SAT: Standardized residuals vs. predicted
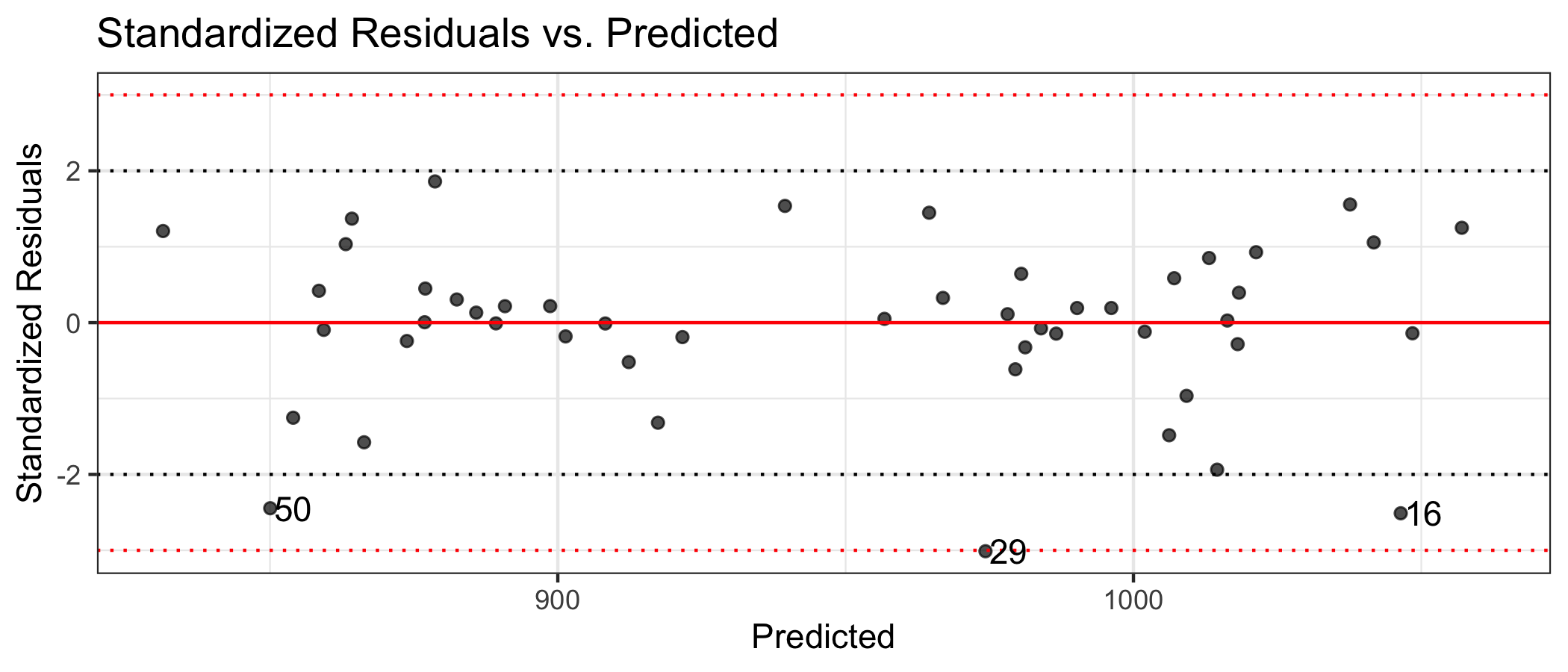
Cook's Distance
Motivating Cook's Distance
An observation's influence on the regression line depends on
How close it lies to the general trend of the data - std.residi
Its leverage - hi
Motivating Cook's Distance
An observation's influence on the regression line depends on
How close it lies to the general trend of the data - std.residi
Its leverage - hi
Cook's Distance is a statistic that includes both of these components to measure an observation's overall impact on the model
Cook's Distance
Cook's distance for the ith observation
Di=(std.resi)2p+1(hi1−hi)
Cook's Distance
Cook's distance for the ith observation
Di=(std.resi)2p+1(hi1−hi)
An observation with large Di is said to have a strong influence on the predicted values
Cook's Distance
Cook's distance for the ith observation
Di=(std.resi)2p+1(hi1−hi)
An observation with large Di is said to have a strong influence on the predicted values
An observation with
- Di>0.5 is moderately influential
- Di>1 is very influential
Cook's Distance
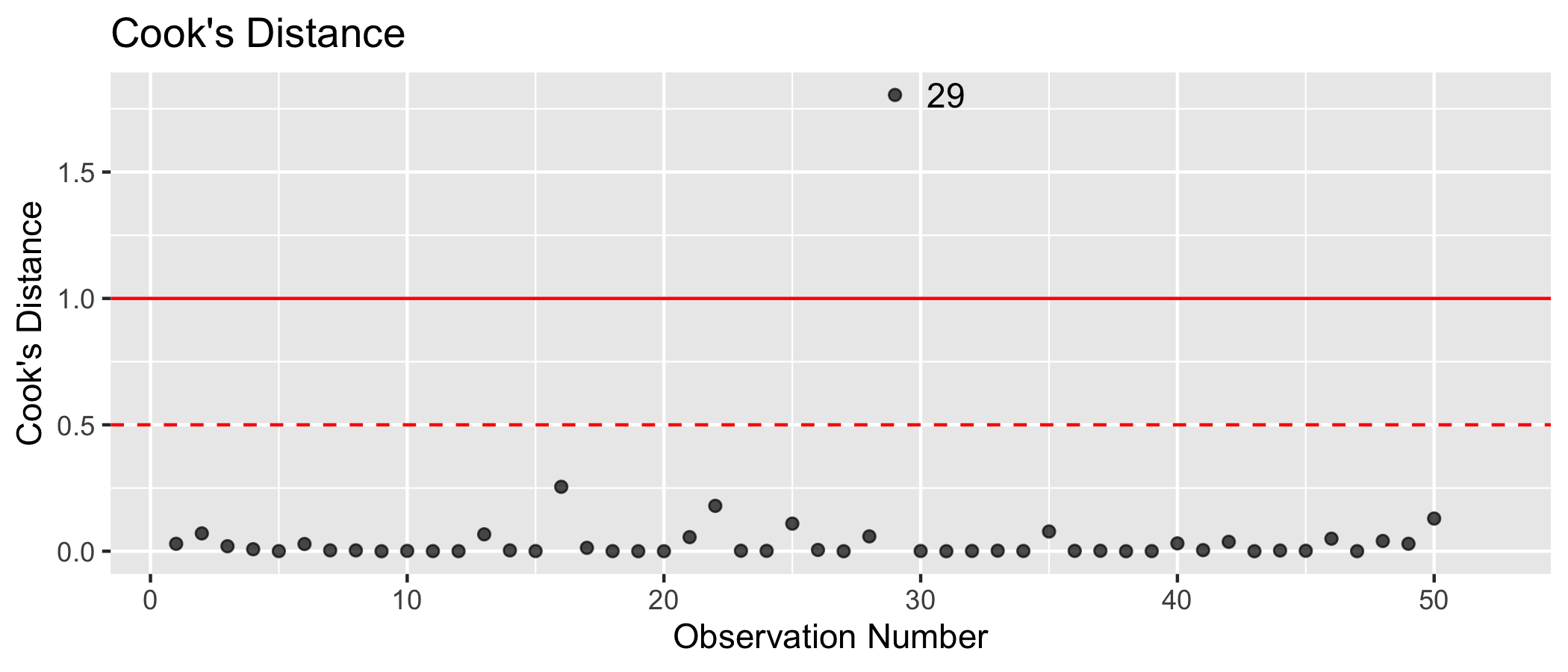
Influential point: Alaska
## # A tibble: 1 x 7## obs_num Takers Income Years Public Expend Rank## <int> <int> <int> <dbl> <dbl> <dbl> <dbl>## 1 29 31 401 15.3 96.5 50.1 79.6Influential point: Alaska
## # A tibble: 1 x 7## obs_num Takers Income Years Public Expend Rank## <int> <int> <int> <dbl> <dbl> <dbl> <dbl>## 1 29 31 401 15.3 96.5 50.1 79.6- high leverage 0.5820757
- large magnitude standardized residual -3.0119952
Model with and without Alaska
With Alaska
| term | estimate |
|---|---|
| (Intercept) | -94.659 |
| Takers | -0.480 |
| Income | -0.008 |
| Years | 22.610 |
| Public | -0.464 |
| Expend | 2.212 |
| Rank | 8.476 |
Model with and without Alaska
With Alaska
| term | estimate |
|---|---|
| (Intercept) | -94.659 |
| Takers | -0.480 |
| Income | -0.008 |
| Years | 22.610 |
| Public | -0.464 |
| Expend | 2.212 |
| Rank | 8.476 |
Without Alaska
| term | estimate |
|---|---|
| (Intercept) | -203.926 |
| Takers | 0.018 |
| Income | 0.181 |
| Years | 16.536 |
| Public | -0.443 |
| Expend | 3.730 |
| Rank | 9.789 |
Using these measures
Standardized residuals, leverage, and Cook's Distance should all be examined together
Examine plots of the measures to identify observations that are outliers, high leverage, and may potentially impact the model.
What to do with outliers/influential points?
It is OK to drop an observation based on the predictor variables if...
It is meaningful to drop the observation given the context of the problem
You intended to build a model on a smaller range of the predictor variables. Mention this in the write up of the results and be careful to avoid extrapolation when making predictions
What to do with outliers/influential points?
It is not OK to drop an observation based on the response variable
These are legitimate observations and should be in the model
You can try transformations or increasing the sample size by collecting more data
What to do with outliers/influential points?
It is not OK to drop an observation based on the response variable
These are legitimate observations and should be in the model
You can try transformations or increasing the sample size by collecting more data
In either instance, you can try building the model with and without the outliers/influential observations
See the supplemental notes Details on Model Diagnostics for more details about standardized residuals, leverage points, and Cook's distance.
Multicollinearity
Why multicollinearity is a problem
We can't include two variables that have a perfect linear association with each other
If we did so, we could not find unique estimates for the model coefficients
Example
Suppose the true population regression equation is y=3+4x
Example
Suppose the true population regression equation is y=3+4x
- Suppose we try estimating that equation using a model with variables x and z=x/10
Example
Suppose the true population regression equation is y=3+4x
- Suppose we try estimating that equation using a model with variables x and z=x/10
ˆy=ˆβ0+ˆβ1x+ˆβ2z=ˆβ0+ˆβ1x+ˆβ2x10=ˆβ0+(ˆβ1+ˆβ210)x
Example
ˆy=ˆβ0+(ˆβ1+ˆβ210)x
Example
ˆy=ˆβ0+(ˆβ1+ˆβ210)x
- We can set ˆβ1 and ˆβ2 to any two numbers such that ˆβ1+ˆβ210=4
Example
ˆy=ˆβ0+(ˆβ1+ˆβ210)x
We can set ˆβ1 and ˆβ2 to any two numbers such that ˆβ1+ˆβ210=4
Therefore, we are unable to choose the "best" combination of ˆβ1 and ˆβ2
Why multicollinearity is a problem
When we have almost perfect collinearities (i.e. highly correlated predictor variables), the standard errors for our regression coefficients inflate
In other words, we lose precision in our estimates of the regression coefficients
This impedes our ability to use the model for inference or prediction
Detecting Multicollinearity
Multicollinearity may occur when...
- There are very high correlations (r>0.9) among two or more predictor variables, especially when the sample size is small
Detecting Multicollinearity
Multicollinearity may occur when...
There are very high correlations (r>0.9) among two or more predictor variables, especially when the sample size is small
One (or more) predictor variables is an almost perfect linear combination of the others
Detecting Multicollinearity
Multicollinearity may occur when...
There are very high correlations (r>0.9) among two or more predictor variables, especially when the sample size is small
One (or more) predictor variables is an almost perfect linear combination of the others
Include a quadratic in the model mean-centering the variable first
Detecting Multicollinearity
Multicollinearity may occur when...
There are very high correlations (r>0.9) among two or more predictor variables, especially when the sample size is small
One (or more) predictor variables is an almost perfect linear combination of the others
Include a quadratic in the model mean-centering the variable first
Including interactions between two or more continuous variables
Detecting multicollinearity in the EDA
✅ Look at a correlation matrix of the predictor variables, including all indicator variables
- Look out for values close to 1 or -1
✅ Look at a scatterplot matrix of the predictor variables
- Look out for plots that show a relatively linear relationship
Detecting Multicollinearity (VIF)
Variance Inflation Factor (VIF): Measure of multicollinearity in the regression model
VIF(ˆβj)=11−R2Xj|X−j
where R2Xj|X−j is the proportion of variation X that is explained by the linear combination of the other explanatory variables in the model.
Detecting Multicollinearity (VIF)
Typically VIF>10 indicates concerning multicollinearity
- Variables with similar values of VIF are typically the ones correlated with each other
Use the vif() function in the rms R package to calculate VIF
VIF For SAT Model
vif(sat_model) %>% tidy() %>% kable()| names | x |
|---|---|
| Takers | 16.478636 |
| Income | 3.128848 |
| Years | 1.379408 |
| Public | 2.288398 |
| Expend | 1.907995 |
| Rank | 13.347395 |
VIF For SAT Model
vif(sat_model) %>% tidy() %>% kable()| names | x |
|---|---|
| Takers | 16.478636 |
| Income | 3.128848 |
| Years | 1.379408 |
| Public | 2.288398 |
| Expend | 1.907995 |
| Rank | 13.347395 |
Takers and Rank are correlated. We need to remove one of these variables and refit the model.
Model without Takers
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -213.754 | 122.238 | -1.749 | 0.087 |
| Income | 0.043 | 0.133 | 0.322 | 0.749 |
| Years | 22.354 | 6.266 | 3.567 | 0.001 |
| Public | -0.559 | 0.559 | -0.999 | 0.323 |
| Expend | 2.094 | 0.824 | 2.542 | 0.015 |
| Rank | 9.803 | 0.872 | 11.245 | 0.000 |
## # A tibble: 1 x 3## adj.r.squared AIC BIC## <dbl> <dbl> <dbl>## 1 0.863 476. 489.Model without Rank
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 535.091 | 164.868 | 3.246 | 0.002 |
| Income | -0.117 | 0.174 | -0.675 | 0.503 |
| Years | 26.927 | 7.216 | 3.731 | 0.001 |
| Public | 0.536 | 0.607 | 0.883 | 0.382 |
| Expend | 2.024 | 0.980 | 2.066 | 0.045 |
| Takers | -3.017 | 0.335 | -9.014 | 0.000 |
## # A tibble: 1 x 3## adj.r.squared AIC BIC## <dbl> <dbl> <dbl>## 1 0.814 491. 505.Recap
Identifying influential points
- Leverage
- Standardized residuals
- Cook's Distance
Multicollinearity